首先回顾一个经典注意力框架，解释如何在视觉场景中展开注意力。受此框架中的注意力提示的启发，我们将设计能够利用这些注意力提示的模型。1964年的Nadaraya-Waston核回归正是具有注意力机制的机器学习的简单演示。然后继续介绍注意力函数，它们在深度学习的注意力模型设计中被广泛使用。

01 注意力提示

自主性的与非自主性的注意力提示解释了人类的注意力的方式，下面来看看如何通过这两种注意力提示，用神经网络来设计注意力机制的框架，

首先，考虑一个相对简单的状况，即只使用非自主性提示。要想将选择偏向于感官输入，则可以简单地使用参数化的全连接层，甚至是非参数化的最大汇聚层或平均汇聚层。

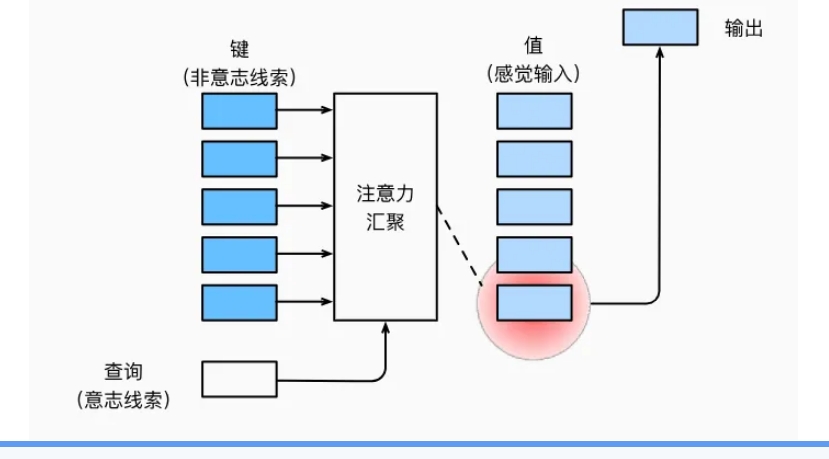
因此，“是否包含自主性提示”将注意力机制与全连接层或汇聚层区别开来。在注意力机制的背景下，自主性提示被称为查询（query）。给定任何查询，注意力机制通过注意力汇聚将选择引导至感官输入，例如中间特征表示。在注意力机制中，这些感官输入被称为值（value）。更通俗的解释，每个值都与一个键（key）配对，这可以想象为感官输入的非自主提示。如图所示，可以通过设计注意力汇聚的方式，便于给定的查询（自主性提示）与键（非自主性提示）进行匹配，这将引导得出最匹配的值（感官输入）。

02  Nadaraya-Watson 核回归

01 生成数据集

简单起见，考虑下面这个回归问题：给定的成对的“输入－输出”数据集

如何学习𝑓来预测任意新输入𝑥的输出𝑦？

根据下面的非线性函数生成一个人工数据集，其中加入的噪声项为𝜖

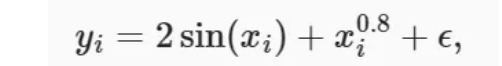
其中𝜖服从均值为0和标准差为0.5的正态分布。在这里生成了50个训练样本和50个测试样本。 

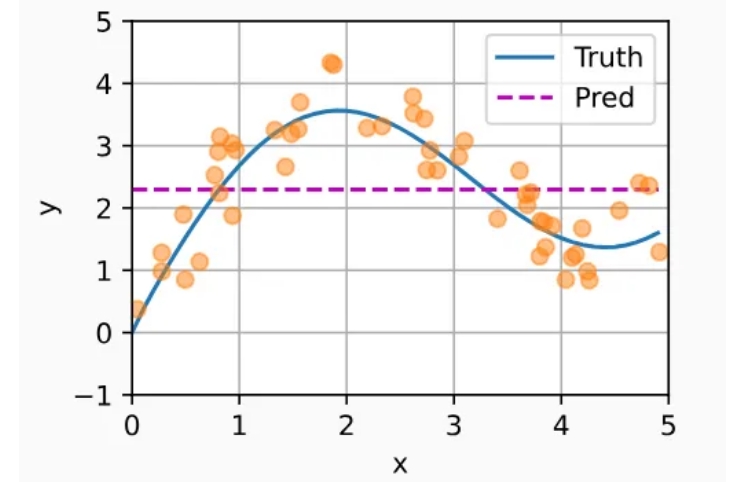
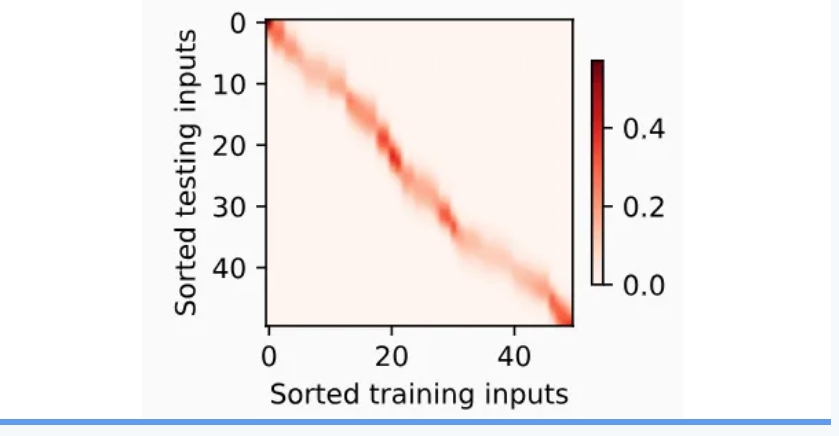
为了更好地可视化之后的注意力模式，需要将训练样本进行排序。将绘制所有的训练样本（样本由圆圈表示），不带噪声项的真实数据生成函数𝑓（标记为“Truth”），以及学习得到的预测函数（标记为“Pred”）。

02 平均汇聚

先使用最简单的估计器来解决回归问题。基于平均汇聚来计算所有训练样本输出值的平均值：

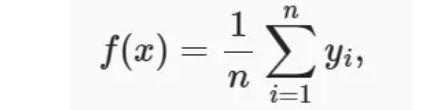
如下图所示，这个估计器确实不够聪明。真实函数𝑓（“Truth”）和预测函数（“Pred”）相差很大。

03 非参数注意力汇聚

显然，平均汇聚忽略了输入𝑥𝑖。于是Nadaraya和Watson提出了一个更好的想法，根据输入的位置对输出𝑦𝑖进行加权：

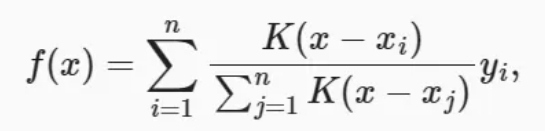
其中𝐾是核（kernel）。公式所描述的估计器被称为 Nadaraya-Watson核回归。这里不会深入讨论核函数的细节，但受此启发，从注意力机制框架的角度重写上述，成为一个更加通用的注意力汇聚公式：

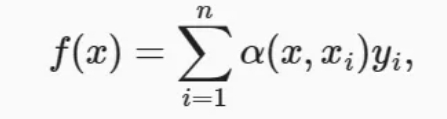
其中𝑥是查询，(𝑥𝑖,𝑦𝑖)是键值对。比较改进前和改进后两个公式，注意力汇聚是𝑦𝑖的加权平均。将查询𝑥和键𝑥𝑖之间的关系建模为注意力权重——𝛼(𝑥,𝑥𝑖)，这个权重将被分配给每一个对应值𝑦𝑖。对于任何查询，模型在所有键值对注意力权重都是一个有效的概率分布：它们是非负的，并且总和为1。

为了更好地理解注意力汇聚，下面考虑一个高斯核（Gaussian kernel），其定义为：

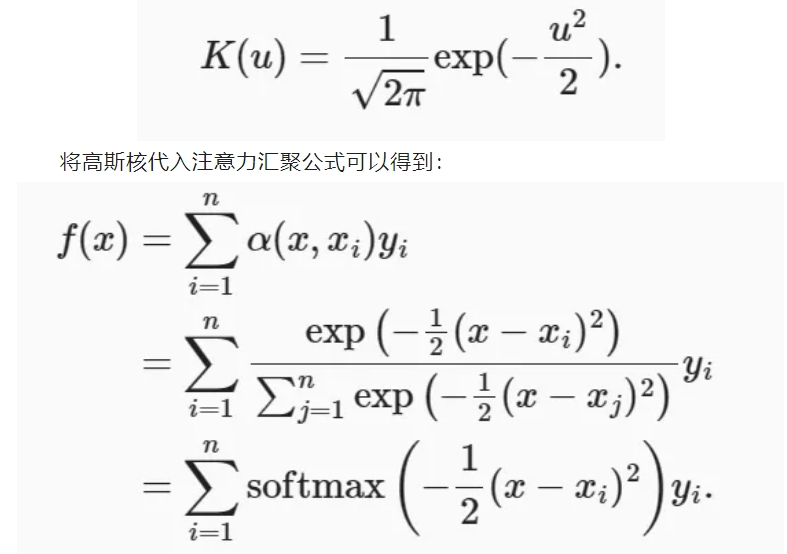
如果一个键𝑥𝑖越是接近给定的查询𝑥，那么分配给这个键对应值𝑦𝑖的注意力权重就会越大，也就“获得了更多的注意力”。

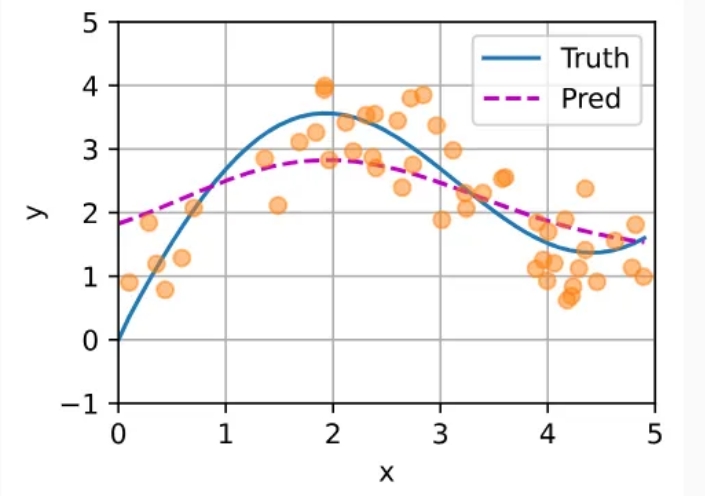
将基于这个非参数的注意力汇聚模型来绘制预测结果。从绘制的结果会发现新的模型预测线是平滑的，并且比平均汇聚的预测更接近真实。

04 带参数注意力汇聚

非参数的Nadaraya-Watson核回归具有一致性的优点：如果有足够的数据，此模型会收敛到最优结果。尽管如此，我们还是可以轻松地将可学习的参数集成到注意力汇聚中。

在下面的查询𝑥和键𝑥𝑖之间的距离乘以可学习参数𝑤：

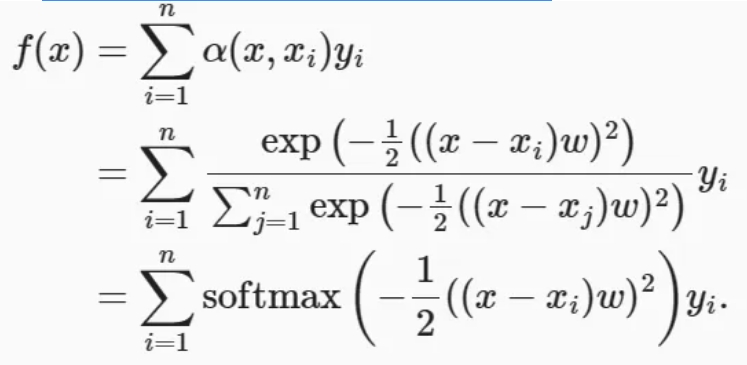
训练完带参数的注意力汇聚模型后可以发现：在尝试拟合带噪声的训练数据时，预测结果绘制的线不如之前非参数模型的平滑。

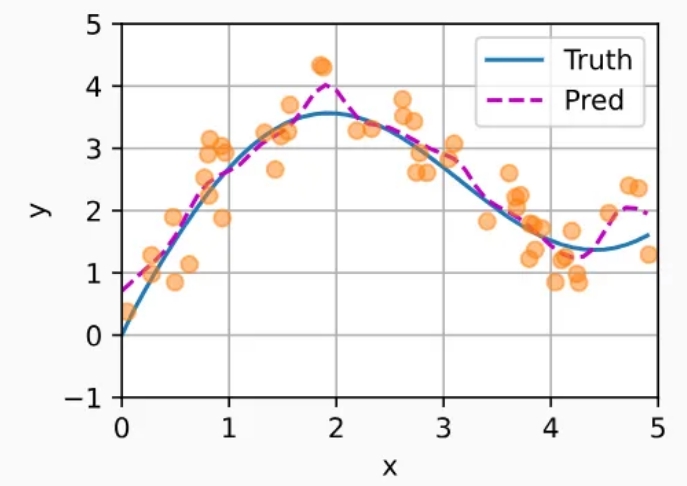
为什么新的模型更不平滑了呢？

带参数的模型加入可学习的参数后，曲线在注意力权重较大的区域变得更不平滑。

03 注意力评分函数

上文中高斯核指数部分可以视为注意力评分函数，简称评分函数，然后把这个函数的输出结果输入到softmax函数中进行运算。通过上述步骤，将得到与键对应的值的概率分布（即注意力权重）。最后，注意力汇聚的输出就是基于这些注意力权重的值的加权和。

从宏观来看，上述算法可以用来实现注意力机制框架。下图说明了如何将注意力汇聚的输出计算成为值的加权和，其中𝑎表示注意力评分函数。由于注意力权重是概率分布，因此加权和其本质上是加权平均值。

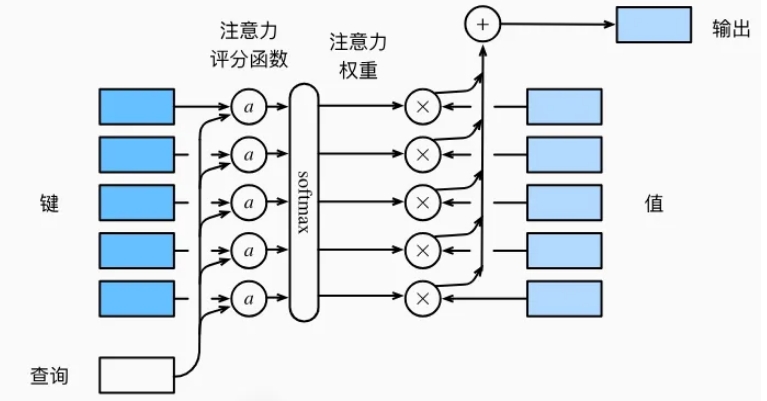
用数学语言描述，假设有一个查询𝑞∈𝑅𝑞和𝑚个“键－值”对(𝑘1,𝑣1),…,(𝑘𝑚,𝑣𝑚)，其中𝑘𝑖∈𝑅𝑘，𝑣𝑖∈𝑅𝑣。注意力汇聚函数𝑓就被表示成值的加权和

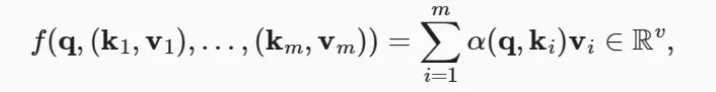
其中查询𝑞和键𝑘𝑖的注意力权重（标量）是通过注意力评分函数𝑎将两个向量映射成标量，再经过softmax运算得到的：

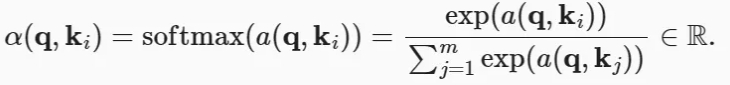
选择不同的注意力评分函数𝑎会导致不同的注意力汇聚操作。本节将介绍两个流行的评分函数，稍后将用他们来实现更复杂的注意力机制。

01 掩码softmax操作

softmax操作用于输出一个概率分布作为注意力权重。在某些情况下，并非所有的值都应该被纳入到注意力汇聚中。例如，为了高效处理小批量数据集，某些文本序列被填充了没有意义的特殊词元。为了仅将有意义的词元作为值来获取注意力汇聚，可以指定一个有效序列长度（即词元的个数），以便在计算softmax时过滤掉超出指定范围的位置。

02 加性注意力

一般来说，当查询和键是不同长度的矢量时，可以使用加性注意力作为评分函数。给定查询𝑞∈𝑅𝑞和k∈𝑅k键𝑘∈𝑅𝑘， 加性注意力的评分函数为：

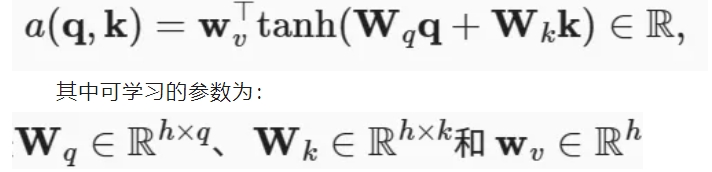
将查询和键连结起来后输入到一个多层感知机（MLP）中，感知机包含一个隐藏层，其隐藏单元数是一个超参数ℎ。通过使用tanh作为激活函数，并且禁用偏置项。

03 缩放点积注意力

使用点积可以得到计算效率更高的评分函数，但是点积操作要求查询和键具有相同的长度𝑑。假设查询和键的所有元素都是独立的随机变量，并且都满足零均值和单位方差，那么两个向量的点积的均值为0，方差为𝑑。为确保无论向量长度如何，点积的方差在不考虑向量长度的情况下仍然是1，我们再将点积除以根号𝑑，则缩放点积注意力评分函数为：

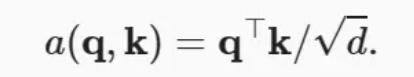
在实践中，我们通常从小批量的角度来考虑提高效率，例如基于𝑛个查询和𝑚个键－值对计算注意力，其中查询和键的长度为𝑑，值的长度为𝑣。查询𝑄∈𝑅𝑛×𝑑、键𝐾∈𝑅𝑚×𝑑和值𝑉∈𝑅𝑚×𝑣的缩放点积注意力是：

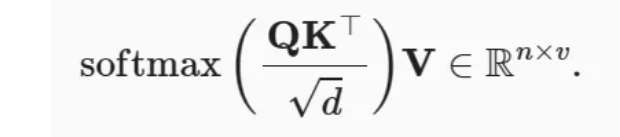
04 多头注意力

在实践中，当给定相同的查询、键和值的集合时，我们希望模型可以基于相同的注意力机制学习到不同的行为，然后将不同的行为作为知识组合起来，捕获序列内各种范围的依赖关系，例如，短距离依赖和长距离依赖关系。因此，允许注意力机制组合使用查询、键和值的不同子空间表示是有益的。

为此，与其只使用单独一个注意力汇聚，我们可以用独立学习得到的ℎ组不同的线性投影来变换查询、键和值。然后，这ℎ组变换后的查询、键和值将并行地送到注意力汇聚中。最后，将这ℎ个注意力汇聚的输出拼接在一起，并且通过另一个可以学习的线性投影进行变换，以产生最终输出。这种设计被称为多头注意力。对于ℎ个注意力汇聚输出，每一个注意力汇聚都被称作一个头（head）。下图展示了使用全连接层来实现可学习的线性变换的多头注意力。

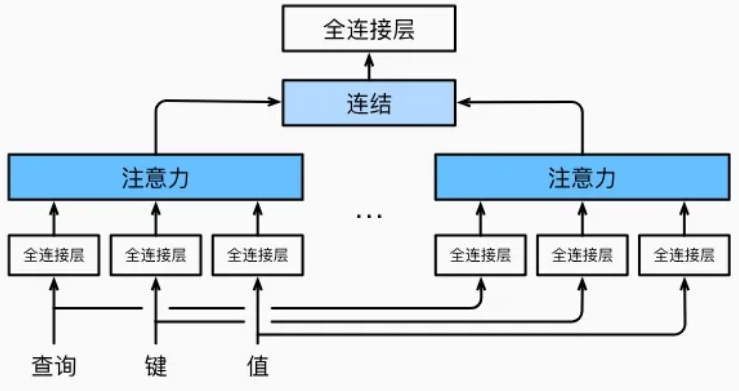
以及代表注意力汇聚的函数𝑓。𝑓可以是加性注意力和缩放点积注意力。多头注意力的输出需要经过另一个线性转换，它对应着ℎ个头连结后的结果，因此其可学习参数是：

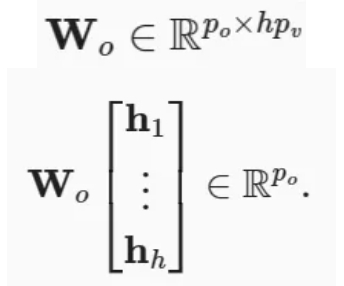
基于这种设计，每个头都可能会关注输入的不同部分， 可以表示比简单加权平均值更复杂的函数。

05 自注意力和位置编码

01 自注意力

给定一个由词元组成的输入序列𝑥1,…,𝑥𝑛，其中任意𝑥𝑖∈𝑅𝑑（1≤𝑖≤𝑛）。该序列的自注意力输出为一个长度相同的序列𝑦1,…,𝑦𝑛，其中：

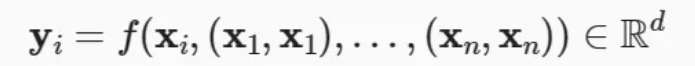
02 位置编码

在处理词元序列时，循环神经网络是逐个的重复地处理词元的，而自注意力则因为并行计算而放弃了顺序操作。为了使用序列的顺序信息，通过在输入表示中添加位置编码（positional encoding）来注入绝对的或相对的位置信息。位置编码可以通过学习得到也可以直接固定得到。接下来描述的是基于正弦函数和余弦函数的固定位置编码：

假设输入表示𝑋∈𝑅𝑛×𝑑 包含一个序列中𝑛个词元的𝑑维嵌入表示。位置编码使用相同形状的位置嵌入矩阵 𝑃∈𝑅𝑛×𝑑输出𝑋+𝑃，矩阵第𝑖行、第2𝑗列和2𝑗+1列上的元素为：

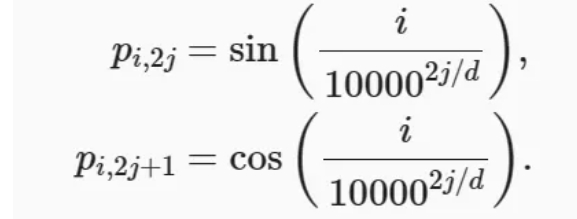
声明：本网站所有相关资料如有侵权请联系站长删除，资料仅供用户学习及研究之用，不构成任何投资建议！