本文探讨了《The Verge》,旨在通过 Verkle 树、STARK 证明、zk 友好的共识机制、Beam 链等技术,提升以太坊的可验证性、可扩展性和可持续性。
可验证性的路径
Web3 的核心优势是可验证性——用户可以验证系统的实际运行方式。这一特性解释了为什么许多人在加密行业内外都将 Web3 视为迈向更加透明和可验证互联网的一步。
与 Web2 平台(如 Facebook 或 Instagram)不同,后者的算法和规则即使经过记录,也依然保持不透明;而加密协议则设计为具备完全的可审计性。即便它们被分享,用户也缺乏验证平台是否按预期运行的能力。这与加密完全相反,加密协议的每一项设计都尽可能确保可审计——至少在理论上是如此。
今天,我们将探讨《The Verge》这一部分内容,分析以太坊在实现未来可验证性、可持续性和可扩展性方面所采取的步骤。本文将讨论如何通过区块链架构使其更加可验证,这些变化在协议层面带来了哪些创新,以及它们如何为用户提供更加安全的生态系统。让我们开始吧!
什么是“可验证性”?
Web2 应用通常作为“黑箱”运作——用户只能看到输入和输出,而无法了解应用如何实际运作。相比之下,加密货币协议通常会公开其源代码,或者至少有计划这样做。这种透明性有两个目的:首先,它允许用户在选择时直接与协议的代码进行互动;其次,它帮助用户准确理解系统如何运作以及哪些规则在其中发挥作用。
“去中心化你能去的部分,其余部分确保可验证。”
可验证性确保系统能够承担责任,并且在许多情况下,保证协议按预期运行。这个原则强调最小化中心化的重要性,因为中心化往往导致不透明和无法追责的结构,用户无法验证操作的真实性。相反,我们应当尽可能地实现去中心化,而对于无法去中心化的部分,则应确保其可验证且可追责。
以太坊社区似乎与这种观点一致,因为其路线图中包含了一个名为“Verge”的里程碑,旨在让以太坊变得更加可验证。然而,在深入探讨《The Verge》之前,我们需要了解区块链的哪些方面应该被验证,以及从用户的角度来看,哪些部分是至关重要的。
区块链本质上充当了全球时钟的角色。在一个由大约 10,000 台计算机组成的分布式网络中,交易从源节点传播到所有其他节点可能需要相当长的时间。因此,网络中的节点无法确定交易的确切顺序——即无法判断某笔交易是先到达还是后到达,因为它们只能从自身的主观视角进行观察。
由于交易顺序非常重要,区块链网络使用称为“共识算法”的专门方法,确保节点保持同步并按照相同的顺序处理交易序列。尽管节点无法在全球范围内确定交易的顺序,但共识机制使得所有节点能够达成一致,确认相同的交易序列,从而使整个网络像一个单一且协调的计算机一样运作。
除了共识层之外,每个区块链中还有一个执行层。执行层由用户想要执行的交易所决定。 \
一旦交易通过共识成功排序,每笔交易就必须应用于执行层的当前状态。如果你在想,“什么是状态?”那么你可能已经看到区块链被比作数据库——或者更具体地说,是银行的数据库,因为区块链与银行一样,会记录每个人的账户余额。
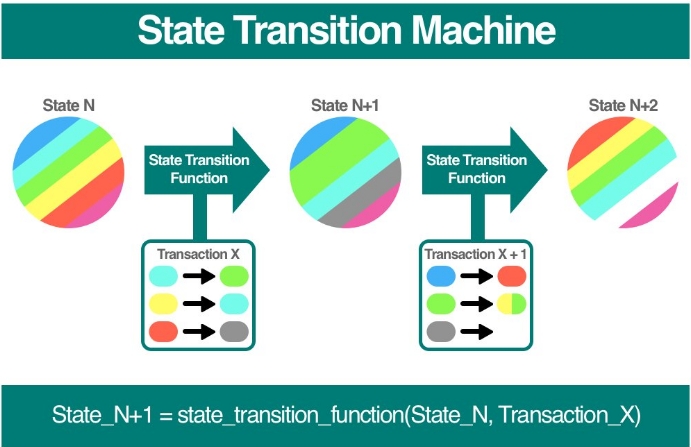
如果你在状态“S”中有 $100,并且想要向其他人发送 $10,那么在下一个状态“S+1”中,你的余额将变为 $90。这一过程,即通过应用交易从一个状态过渡到另一个状态的过程,我们称之为 STF(状态转换函数)。
在比特币中,STF 主要限于余额变化,因此相对简单。然而,与比特币不同,Ethereum 的 STF 要复杂得多,因为以太坊是一个完全可编程的区块链,具有执行层,能够运行代码。
在区块链中,有三个基本组件是你需要或能够验证的:
状态:你可能想读取区块链上的某一数据,但由于你没有运行完整节点,因此无法直接访问该状态。因此,你通过像 Alchemy 或 Infura 这样的 RPC(远程过程调用)提供者请求数据。然而,你必须验证这些数据在 RPC 提供者处未被篡改。
执行:如前所述,区块链利用 STF。你必须验证状态转换是否正确执行——这不是逐笔交易地验证,而是逐块地验证。
共识:像 RPC 这样的第三方实体可以提供你尚未被包含在区块链中的有效区块。因此,你必须验证这些区块已经通过共识被接受,并且被添加到区块链中。
如果这些内容听起来令人困惑或不清楚,不用担心,我们将详细解释每个方面。首先,让我们从如何验证区块链状态开始!
如何验证区块链状态?
以太坊的“状态”指的是区块链在任何特定时间点存储的数据集合。这些数据包括账户余额(包括合约账户和外部拥有账户,简称 EOA)、智能合约代码、合约存储等。以太坊是一个基于状态的机器,因为在以太坊虚拟机(EVM)中处理的每一笔交易都会改变先前的状态,并产生一个新的状态。
每个以太坊区块都包含一个值,用于总结该区块之后网络的当前状态,这个值称为 stateRoot。这个值是对整个以太坊状态的紧凑表示,通常是一个 64 字符的哈希值。
随着每一笔新交易修改状态,后续区块中记录的 stateRoot 会相应更新。为了计算这个值,以太坊的验证者使用了 Keccak 哈希函数和一种称为 Merkle Tree(默克尔树)的数据结构来组织和总结状态的不同部分。
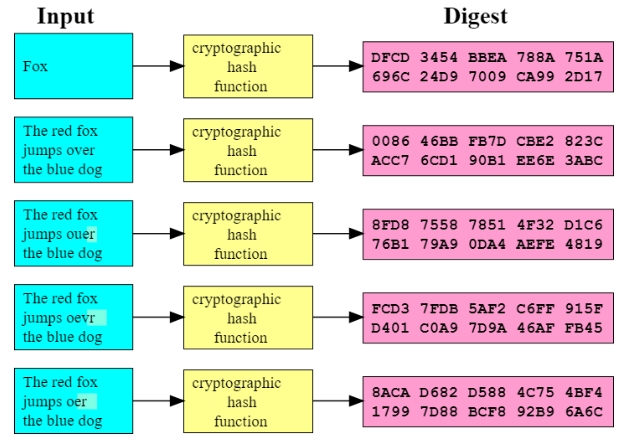
哈希函数是单向函数,它将输入转化为固定长度的输出。在以太坊中,像 Keccak 这样的哈希函数被用来生成数据的摘要,充当输入数据的指纹。哈希函数有四个基本特性:
确定性:相同的输入总是会生成相同的输出。
固定输出长度:无论输入的长度如何,输出的长度总是固定的。
单向性:从输出推导出原始输入几乎是不可能的。
唯一性:即使输入发生微小变化,输出也会完全不同。因此,特定的输入会映射到一个几乎唯一的输出。
正因为这些特性,以太坊验证者能够执行每个区块的 STF(状态转换函数)——执行区块中的所有交易并将其应用到状态中,然后验证区块中指示的状态是否与通过 STF 得到的状态匹配。这个过程确保了区块提议者的诚实行为,使其成为验证者的核心职责之一。
然而,以太坊验证者并不会直接对整个状态进行哈希操作来找到其摘要。由于哈希函数的单向特性,直接对状态进行哈希会消除可验证性,因为重现该哈希的唯一方法是拥有整个状态。
由于以太坊的状态数据量达到数 TB,因此将整个状态存储在手机或个人计算机等日常设备上是不切实际的。为了解决这个问题,以太坊使用 Merkle 树 结构来计算 stateRoot,尽可能保留状态的可验证性。
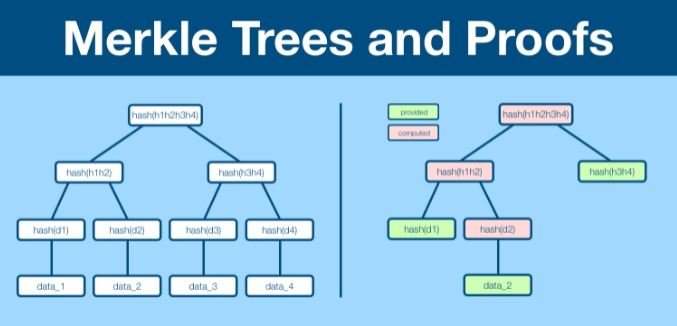
Merkle 树是一种加密数据结构,用于安全且高效地验证数据的完整性和正确性。Merkle 树基于哈希函数构建,将数据集的哈希值按照层级结构组织,从而使得能够验证数据的完整性和正确性。该树结构由三种类型的节点组成:
叶子节点:这些节点包含单个数据片段的哈希值,位于树的最底层。每个叶子节点代表 Merkle 树中某一特定数据片段的哈希值。
分支节点:这些节点包含其子节点的组合哈希值。例如,在一个二叉 Merkle 树中(N=2),两个子节点的哈希值会被连接起来,再次进行哈希运算,生成一个分支节点的哈希值,位于更高的层级。
根节点:根节点位于 Merkle 树的最顶层,代表整个树的加密摘要。这个节点用于验证树中所有数据的完整性和正确性。
如果你想知道如何构建这样的树,实际上它只需要两个简单的步骤:
叶子节点创建:每个数据片段通过哈希函数进行处理,得到的哈希值形成叶子节点。这些节点位于树的最底层,代表数据的加密摘要。
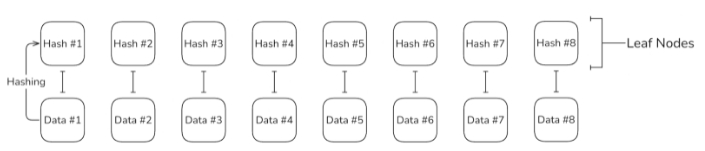
叶子节点的哈希值会按一定方式(例如按对组)进行分组和合并,随后进行哈希运算。这个过程会在树的下一层生成分支节点。对于每个分支节点,重复相同的过程,直到只剩下一个哈希值。
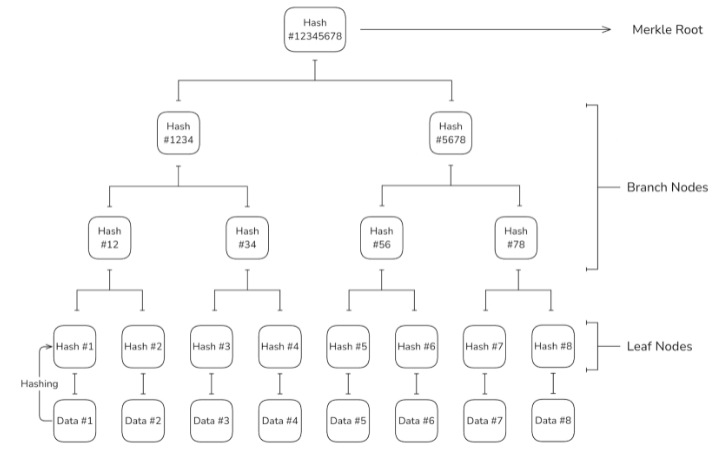
最终,在树顶端获得的哈希值被称为 Merkle 根。Merkle 根代表整个树的加密摘要,并允许安全地验证数据的完整性。
我们如何使用 Merkle 根来验证以太坊的状态?
Merkle 证明 使得验证者能够高效地验证特定数据片段的有效性,通过提供一系列哈希值,形成从目标数据(即叶子节点)到区块头中存储的 Merkle 根的路径。这个中间哈希链使得验证者能够确认数据的真实性,而无需对整个状态进行哈希计算。
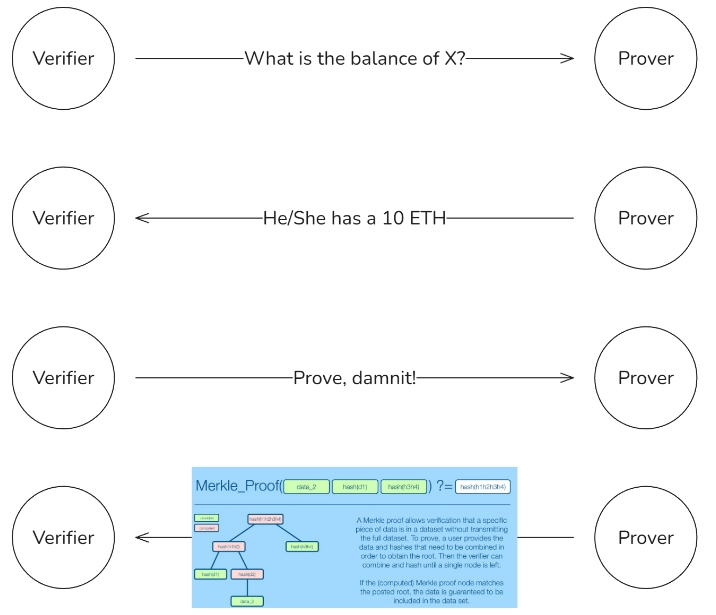
验证者从特定的数据点开始,将其与 Merkle 证明中提供的每个“兄弟”哈希值逐步合并,并进行哈希运算。这一过程会一直持续,直到产生一个单一的哈希值。如果计算出的哈希值与存储的 Merkle 根匹配,则数据被视为有效;否则,验证者可以确定该数据与所声明的状态不符。
示例:使用 Merkle 证明验证数据点
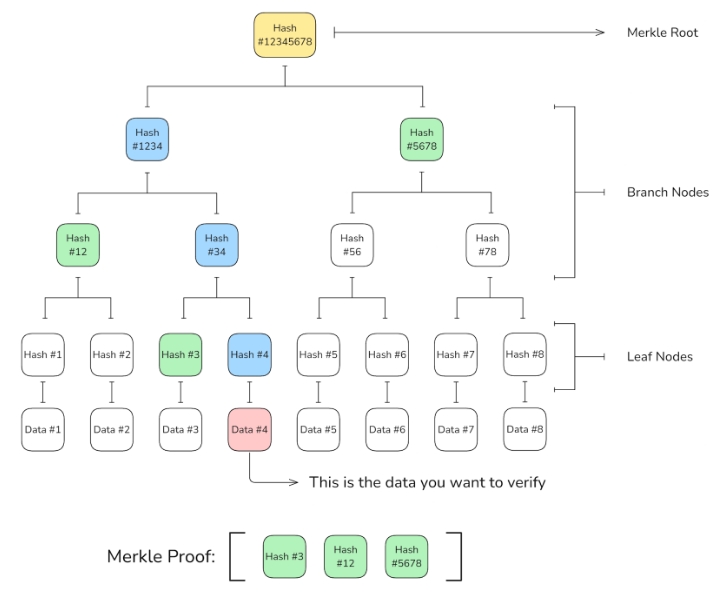
假设我们从 RPC 接收到数据 #4,并希望使用 Merkle 证明验证其真实性。为此,RPC 会提供一组哈希值,这些哈希值形成一条路径,能够达到 Merkle 根。对于数据 #4,兄弟哈希值将包括 Hash #3、Hash #12 和 Hash #5678。
从数据 4 开始:首先,我们对数据 #4 进行哈希,得到 Hash #4。
与兄弟节点合并:然后,我们将 Hash #4 与 Hash #3(它在叶子层级的兄弟节点)合并,并进行哈希运算,得到 Hash #34。
向上移动树:接下来,我们将 Hash #34 与 Hash #12(它在下一层的兄弟节点)合并,并哈希得到 Hash #1234。
最后一步:最后,我们将 Hash #1234 与 Hash #5678(提供的最后一个兄弟哈希)合并,并进行哈希运算。结果哈希应该与存储在区块头中的 Merkle 根(Hash #12345678)匹配。
如果计算出的 Merkle 根与区块中的状态根匹配,那么我们确认数据 #4 在该状态下是有效的。如果不匹配,则说明数据不属于所声明的状态,表明可能存在篡改。正如你所看到的,验证者无需提供所有数据的哈希值,也不需要从头开始重建整个 Merkle 树,仅通过提供三个哈希值,证明者就能证明数据 #4 在该状态中存在且未被篡改。这就是为什么 Merkle 证明被认为是高效的主要原因。
Merkle 树的效率是否足够高?
虽然 Merkle 树无疑在像以太坊这样的大型区块链系统中提供了安全且高效的数据验证,但它们是否真的足够高效呢?为了回答这个问题,我们必须分析 Merkle 树的性能和大小如何影响证明者与验证者之间的关系。
影响 Merkle 树性能的两个关键因素
分支因子:每个分支节点的子节点数量。
数据总大小:树中表示的数据集的大小。
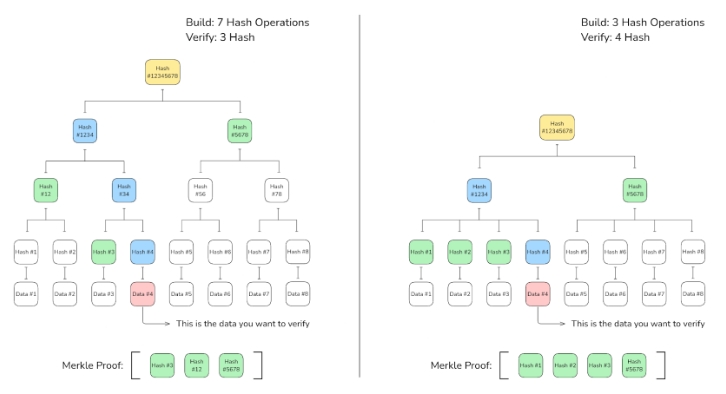
分支因子的影响
为了更好地理解分支因子的影响,我们来举一个例子。分支因子决定了每个节点会从多少个分支延伸出去。
小的分支因子(例如,二叉 Merkle 树)
如果使用的是二叉 Merkle 树(分支因子为 2),那么证明的大小非常小,使得验证过程对验证者来说更加高效。在每个节点只有两个分支的情况下,验证者只需要处理每一层的一个兄弟哈希。这加快了验证速度,并减少了计算负担。然而,较小的分支因子增加了树的高度,在构建树时需要更多的哈希操作,这对验证者来说可能是一个负担。
较大的分支因子(例如,4)
较大的分支因子(例如,4)降低了树的高度,形成了一个更短、更宽的结构。由于需要的哈希操作较少,完整节点(Full Nodes)能够更快地构建树。然而,对于验证者来说,这会增加他们在每一层需要处理的兄弟哈希数量,导致证明的大小变大。每次验证步骤中需要更多的哈希值,也意味着验证者的计算和带宽成本更高,实际上将负担从验证者转移到了验证者身上。
总结来说,较大的分支因子通过降低树的高度和构建时间来提高了验证速度,但同时也增加了验证时的工作量和资源消耗。因此,在设计 Merkle 树时,需要平衡分支因子的大小,以实现验证效率和构建效率之间的最佳折衷。
第二章:以太坊可验证性革命——The Verge
The Verge 是以太坊路线图中的一个里程碑,旨在提高可验证性,强化区块链的去中心化结构,并增强网络安全性。以太坊网络的一个主要目标是使任何人都能轻松运行验证节点来验证区块链,创建一个没有中心化的开放参与结构。这一验证过程的可达性是区块链区别于中心化系统的关键特征之一。虽然中心化系统不提供验证功能,但区块链的正确性完全掌握在其用户手中。然而,为了保持这一保证,运行一个验证节点必须对所有人都能访问——这是当前系统下的一个挑战,因为验证节点需要大量的存储和计算资源。
自从通过 The Merge 转向 权益证明(Proof-of-Stake,PoS) 共识模型以来,以太坊验证者有两个主要责任:
确保共识:支持概率性和确定性共识协议的正常运行,并应用分叉选择算法。
检查区块准确性:在执行区块中的交易后,验证结果状态树的根是否与提议者声明的状态根匹配。
为了履行第二项责任,验证者必须能够访问区块之前的状态。这使得他们能够执行区块中的交易,并推导出后续状态。然而,这一要求给验证者带来了沉重的负担,因为他们需要处理大量的存储要求。虽然以太坊的设计目标是使其可行,并且全球存储成本正在逐渐降低,但问题的关键不在于成本,而在于验证者需要依赖专用硬件。The Verge 旨在通过创建一个基础设施来克服这一挑战,使得即使在存储有限的设备上(如手机、浏览器钱包,甚至智能手表)也能进行完整的验证,允许验证节点在这些设备上运行。
可验证性的第一步:状态
过渡到 Verkle 树 是这个过程的关键部分。最初,The Verge 的重点是将以太坊的 Merkle 树结构替换为 Verkle 树。采用 Verkle 树的主要原因是,Merkle 树对以太坊可验证性构成了重大障碍。虽然在正常情况下,Merkle 树及其证明能够高效地工作,但在最坏的情况下,它们的性能会急剧下降。
根据 Vitalik 的计算,平均证明大小约为 4 KB,这听起来是可以管理的。然而,在最坏的情况下,证明的大小可能会膨胀到 330 MB。是的,你没看错——330 MB。
以太坊的 Merkle 树在最坏情况下的极端低效,主要源于两个原因:
使用十叉树(Hexary Trees)
目前,以太坊使用的 Merkle 树的分支因子是 16。这意味着,验证一个单独的节点时,需要提供该分支中的其他 15 个哈希。考虑到以太坊状态的大小和分支数量,在最坏的情况下,这会造成相当大的负担。

非 Merkle 化的代码:以太坊并没有将合约代码纳入树结构,而是将代码进行哈希处理,并使用生成的哈希值作为节点。考虑到合约的最大大小为 24 KB,这种方法在实现完全可验证性时会带来显著的负担。
证明大小与分支因子成正比。减少分支因子可以减小证明大小。为了解决这些问题并改善最坏情况下的表现,以太坊可以将十叉树(Hexary Trees)转换为二叉 Merkle 树(Binary Merkle Trees),并开始将合约代码进行 Merkle 化。如果以太坊的分支因子从 16 降到 2,并且将合约代码也进行 Merkle 化,那么最大证明大小可能缩小至 10 MB。虽然这是一个显著的改进,但值得注意的是,这个成本仅适用于验证单个数据。即便是一个简单的交易,访问多个数据项时,也需要更大的证明。考虑到每个区块的交易数量以及以太坊状态的持续增长,尽管这种方案更好,但仍然不完全可行。
因此,以太坊社区提出了两种不同的解决方案来应对这一问题:
Verkle 树
STARK 证明 + 二叉 Merkle 树
Verkle 树与向量承诺(Vector Commitments)

顾名思义,Verkle 树 是类似于 Merkle 树 的树结构。然而,它们在验证过程中的效率方面存在显著差异。在 Merkle 树 中,如果一个分支包含 16 个数据项,且我们只想验证其中的一个数据项,则必须提供覆盖其他 15 个数据项的哈希链。这大大增加了验证的计算负担,并导致了较大的证明大小。
相比之下,Verkle 树 使用了一种名为“基于椭圆曲线的向量承诺(Elliptic Curve-based Vector Commitments)”的专门结构,具体来说,是 基于内积论证(IPA) 的向量承诺。向量本质上是按特定顺序组织的数据元素列表。以太坊的状态可以被视为一个向量:这是一个存储着多个数据项并按特定顺序排列的结构,其中每个元素都至关重要。该状态包含了各种数据组件,例如地址、合约代码和存储信息,而这些元素的顺序在访问和验证过程中起着至关重要的作用。
向量承诺是用于证明和验证数据集内数据元素的密码学方法。这些方法能够同时验证数据集内每个元素的存在性和顺序。例如,Merkle Proofs(用于 Merkle 树)也可以视为一种向量承诺形式。虽然 Merkle 树需要验证元素时提供所有相关的哈希链,但其结构本质上证明了向量中的所有元素是按特定顺序相连接的。
与 Merkle 树不同,Verkle 树采用了基于椭圆曲线的向量承诺,这为其提供了两个主要优势:
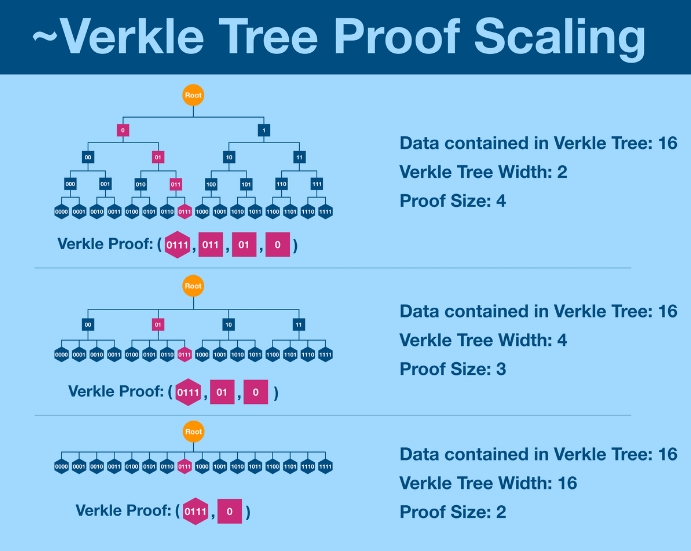
基于椭圆曲线的向量承诺 消除了验证数据时需要提供与被验证数据无关的其他元素的细节。在 Merkle 树 中,若采用 16 分支因子,验证单一分支时需要提供其他 15 个哈希值。考虑到以太坊的状态庞大且包含多个分支,这种做法会造成极大的低效性。而 基于椭圆曲线的向量承诺 则消除了这种复杂性,它允许通过较少的数据和计算工作量完成验证。
通过 多重证明(multi-proofs),基于椭圆曲线的向量承诺所生成的证明可以被压缩成一个恒定大小的证明。由于以太坊的状态不仅庞大,而且持续增长,随着时间的推移,需要验证的分支数量也在增加。然而,使用 Verkle 树 后,我们可以利用 Dankrad Feist 文章中详细描述的方法,将每个分支的证明“压缩”成一个单一的恒定大小的证明。这样,验证者只需要使用一个小的证明来验证整个树,而不必单独验证每一个分支。这也意味着,Verkle 树不会受到以太坊状态增长的影响。
基于椭圆曲线的向量承诺的这些特点大大减少了验证所需的数据量,使 Verkle 树即使在最坏的情况下也能产生小而恒定大小的证明,从而最小化了数据开销和验证时间,提高了像以太坊这样的庞大网络的效率。因此,Verkle 树中的椭圆曲线向量承诺使得以太坊日益增长的状态能够更有效地管理和处理。
Verkle 树的局限性
然而,像所有创新一样,Verkle 树也有其局限性。其中一个主要缺点是它依赖于 椭圆曲线加密,这使其面临量子计算机的潜在威胁。量子计算机比经典计算方法拥有更强大的计算能力,这对椭圆曲线加密协议构成了显著威胁。量子算法可能会打破或削弱这些加密系统,引发对 Verkle 树长期安全性的担忧。
因此,尽管 Verkle 树为实现无状态性(statelessness)提供了有前景的解决方案,但它们并不是最终的解决办法。然而,像 Dankrad Feist 这样的专家强调,虽然在将量子抗性加密技术整合到以太坊中时需要谨慎考虑,但值得注意的是,目前以太坊中用于 blob 的 KZG 承诺同样并不具备量子抗性。因此,Verkle 树可以作为一个过渡性解决方案,为以太坊网络提供更多时间来开发更强大的替代方案。
STARK 证明 + 二叉 Merkle 树
Verkle 树通过提供更小的证明大小和更高效的验证过程,相较于传统的 Merkle 树,更容易管理以太坊不断增长的状态。得益于 基于椭圆曲线的向量承诺,Verkle 树可以用显著更少的数据生成大规模的证明。然而,尽管 Verkle 树在效率上有诸多优势,其对量子计算机的脆弱性使得它们只能作为暂时的解决方案。虽然以太坊社区将 Verkle 树视为短期工具,以买时间应对长期解决方案的到来,但长远目标是向抗量子计算的解决方案过渡。在这一背景下,STARK 证明 和 二叉 Merkle 树 提供了一个强有力的替代方案,旨在为未来构建更强大的可验证性基础设施。
在以太坊的状态验证过程中,通过使用 二叉 Merkle 树,可以将 Merkle 树的分支因子从 16 减少到 2。这个改变对于减少证明大小并提高验证效率至关重要。然而,即便是在最坏的情况下,证明大小仍然可能达到 10 MB,这依然是相当庞大的。此时,STARK 证明 就发挥了作用,它能够将这些大型的二叉 Merkle 证明压缩到仅 100-300 KB。
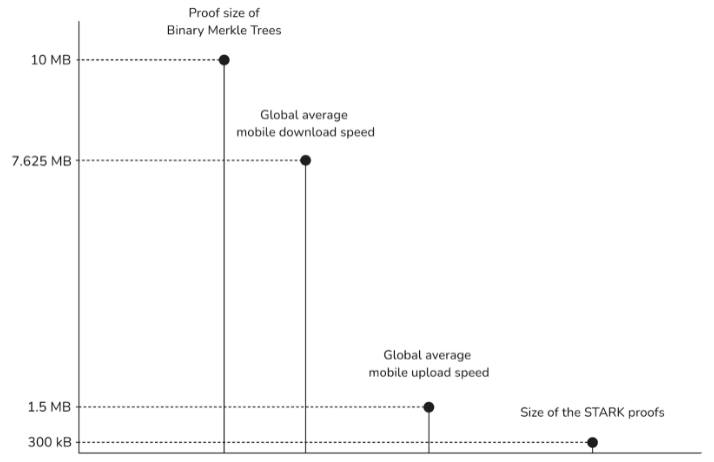
这种优化对于在轻客户端或硬件受限的设备上操作验证者尤其重要,尤其是在考虑到全球平均的移动下载和上传速度大约分别为 7.625 MB/s 和 1.5 MB/s 的情况下。用户可以通过小巧且便于携带的证明验证交易,而无需访问完整的状态;验证者则可以在不存储整个状态的情况下执行区块验证任务。
这种双重优化方案同时减少了验证者的带宽和存储需求,加速了验证过程,带来了三个关键的改进,直接支持了以太坊对于 可扩展性 的愿景:
减少带宽需求:STARK 证明压缩了证明大小,降低了网络传输的带宽需求,使得验证者和用户能够更高效地进行数据传输和验证。
减少存储需求:验证者无需存储整个状态,而是通过小型的证明来验证区块和交易的有效性,从而减少了存储压力。
加速验证过程:较小的证明使得验证过程更加高效,尤其是对于轻客户端而言,可以大大提升用户体验并减少计算负担。
这种组合方案不仅提升了验证的效率,还为以太坊的 可扩展性 提供了强有力的支持,特别是在面对大量交易和不断扩展的区块链状态时。通过使用 STARK 证明 和 二叉 Merkle 树,以太坊能够实现更高效、更经济的状态验证,同时为将来抗量子计算的加密技术铺平道路。
STARK 证明的主要挑战:
证明方的高计算负载:
生成 STARK 证明的过程在计算上非常密集,特别是在证明方这一侧,这可能导致操作成本的增加。
小数据证明的低效率:
虽然 STARK 证明在处理大规模数据集时表现出色,但在证明少量数据时却较为低效,这可能会限制其在某些场景中的应用。当处理涉及较小步骤或数据集的程序时,STARK 证明的相对较大证明大小可能使其在这些情况下不够实用或成本效益低。
量子安全带来的代价:证明方的计算负载
一个区块的 Merkle 证明可能包含大约 330,000 个哈希值,在最坏的情况下,这个数字可能增加到 660,000。在这种情况下,STARK 证明需要每秒处理约 200,000 个哈希值。
在这里,像 Poseidon 这样的 zk 友好哈希函数发挥了作用,它们专门优化了 STARK 证明的计算负载。Poseidon 被设计为比传统哈希算法(如 SHA256 和 Keccak)更适合与 ZK 证明配合使用。其主要原因在于传统哈希算法的工作方式:它们将输入处理为二进制数据(0 和 1)。而 ZK 证明则使用素数域,这是一种在数学上根本不同的结构。这种情况类似于计算机在二进制系统中运行,而人类在日常生活中使用十进制系统。将基于位的数据转换为 ZK 兼容的格式会涉及大量的计算开销。Poseidon 通过本地在素数域内操作,极大地加速了与 ZK 证明的集成。
然而,由于 Poseidon 是一种相对较新的哈希函数,它需要更广泛的安全性分析,以建立与传统哈希函数(如 SHA256 和 Keccak)相同的信任度。为此,以太坊基金会发起了 Poseidon 密码分析计划,邀请专家们对 Poseidon 的安全性进行严格测试和分析,确保其能够经受住敌对审查,并成为加密应用的强健标准。另一方面,像 SHA256 和 Keccak 这样的老旧函数已经经过了广泛的测试,拥有经过验证的安全性记录,但它们并不适合 ZK 使用,这导致在与 STARK 证明配合使用时性能下降。
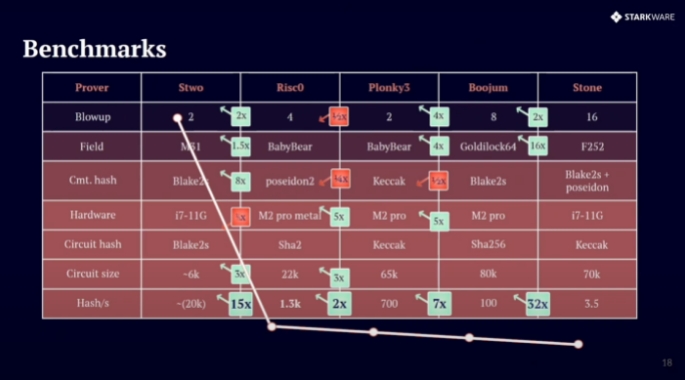
例如,使用传统哈希函数的 STARK 证明目前只能处理 10,000 到 30,000 个哈希值。幸运的是,STARK 技术的进展表明,这一吞吐量很快可能会增加到 100,000 到 200,000 个哈希值,从而显著提高其效率。
STARK 在小数据证明中的低效性
尽管 STARK 证明在大规模数据集的可扩展性和透明性方面表现出色,但在处理小规模且众多的数据元素时,它们显示出了局限性。在这些场景中,证明的数据通常较小,但需要多个证明。以下是一些例子:
账户抽象(AA)交易验证: 使用账户抽象(AA)时,钱包可以指向合约代码,绕过或定制当前以太坊中强制执行的步骤,如非序号和签名验证。然而,这种验证灵活性要求检查合约代码或与交易有效性相关的其他数据。
轻客户端 RPC 调用: 轻客户端从网络查询状态数据(例如,在进行 eth_call 请求时),而无需运行完整节点。为了确保这些状态的正确性,必须支持查询的数据并确认其与网络当前状态相匹配。
包含列表: 较小的验证者可以使用包含列表机制来确保交易包含在下一个区块中,从而限制强大区块生产者的影响。然而,验证这些交易的包含性需要确保它们的正确性。
在这些使用场景中,STARK 证明的优势较小。STARK 强调可扩展性(正如它名字中的 “S” 所表明的那样),适用于大规模数据集,但在小数据场景中却表现不佳。相比之下,SNARK 证明设计强调简洁性(同样是名字中的 “S” 所表示),专注于最小化证明大小,在带宽或存储受限的环境中具有明显的优势。
STARK 证明的大小与 SNARK 证明的对比
STARK 证明通常为 40-50 KB,而 SNARK 证明仅为 288 字节,后者约为前者的 175 倍大。这一大小差异增加了验证时间和网络成本。STARK 证明较大尺寸的主要原因是其依赖于透明性和多项式承诺来确保可扩展性,这在小数据场景中引入了性能开销。在这些情况下,像 Merkle Proof 这样的更快速、更节省空间的方法可能会更加实用。Merkle Proof 提供低计算成本和快速更新,使其在这些场景中更为合适。
然而,尽管 STARK 证明在小数据证明中相对低效,但由于其量子安全性,它们仍然对以太坊的无状态未来至关重要。

如表格所总结的,以太坊有四条潜在的技术路径可以选择:
1. Verkle 树
Verkle 树得到了以太坊社区的广泛支持,社区每两周举行会议来推动其发展。得益于持续的工作和测试,Verkle 树在目前的替代方案中,是最成熟且研究最深入的解决方案。此外,Verkle 树具有加法同态特性,这意味着在更新状态根时,无需重新计算每个分支,相比 Merkle 树,Verkle 树在效率上有所提升。与其他解决方案相比,Verkle 树强调简单性,遵循工程原则,例如“保持简单”或“简单是最好的”,这种简单性有助于它们更容易集成到以太坊中,同时也有助于安全性分析。
然而,Verkle 树并不具备抗量子能力,这使得它们无法作为长期解决方案。如果集成到以太坊中,预计在未来需要被替换,特别是当需要量子抗性解决方案时。即使是 Vitalik 也将 Verkle 树视为一种临时措施,用来为 STARKs 和其他技术提供更多时间以成熟。此外,Verkle 树中使用的基于椭圆曲线的向量承诺,相较于简单的哈希函数,带来了更高的计算负载。基于哈希的方法可能会为全节点提供更快的同步时间。此外,Verkle 树依赖于大量的 256 位运算,这使得它们在现代证明系统中通过 SNARKs 证明变得更加困难,也为未来减少证明大小的工作增添了复杂性。
然而,值得注意的是,Verkle 树由于不依赖哈希,相较于 Merkle 树,其可证明性要强得多。
2. STARKs + 保守哈希函数
将 STARKs 与经过充分验证的保守哈希函数(如 SHA256 或 BLAKE)结合,提供了一个增强以太坊安全性的稳健解决方案。这些哈希函数在学术界和实际应用中得到了广泛使用,并经过了大量的测试。此外,它们的抗量子能力增强了以太坊对量子计算机威胁的抵御能力。在对安全性要求高的场景中,这种组合提供了一个可靠的基础。
然而,使用保守哈希函数的 STARK 系统带来了显著的性能限制。由于这些哈希函数的计算需求较高,证明生成的延迟时间超过 10 秒。这在需要低延迟的场景(如区块验证)中是一个重大缺点。尽管像多维 Gas 提案这样的工作尝试对最坏情况和平均情况的延迟进行对齐,但结果仍然有限。此外,尽管基于哈希的方法可以促进更快的同步时间,但它们的效率可能与 STARKs 的更广泛可扩展性目标不符。传统哈希函数的长计算时间降低了实际效率,并限制了它们的适用性。
3. STARKs + 相对较新的哈希函数
将 STARKs 与新一代的 STARK 友好型哈希函数(例如 Poseidon)结合,显著提高了这种技术的性能。这些哈希函数被设计成能够无缝集成到 STARK 系统中,并大幅度降低证明者延迟。与传统哈希函数不同,它们能够在 1 到 2 秒内生成证明。它们的高效性和低计算开销增强了 STARKs 的可扩展性,使其在处理大规模数据集时表现得尤为高效。这种能力使它们在需要高性能的应用中非常具有吸引力。
然而,这些哈希函数相对较新,需要进行广泛的安全分析和测试。由于缺乏全面的测试,引入这些哈希函数可能会带来风险,尤其是在考虑将其应用于像以太坊这样的关键生态系统时。此外,由于这些哈希函数尚未得到广泛采用,所需的测试和验证过程可能会推迟以太坊可验证性的目标。确保其安全性所需的时间,可能会使这个选项在短期内不那么具有吸引力,进而推迟以太坊的可扩展性和可验证性目标的实现。
4. 基于格的 Merkle 树
基于格的 Merkle 树提供了一个前瞻性的解决方案,将量子安全性与 Verkle 树的更新效率相结合。这些结构解决了 Verkle 树和 STARKs 的弱点,被认为是一个有前景的长期选择。通过其基于格的设计,它们提供了强大的量子计算威胁抵御能力,与以太坊未来证明生态系统的长期需求相契合。此外,通过保留 Verkle 树的更新优势,它们旨在在不牺牲效率的情况下提供更强的安全性。
然而,基于格的 Merkle 树的研究仍处于初期阶段,主要是理论性的。这给它们的实际实现和性能带来了很大的不确定性。将这种解决方案集成到以太坊中将需要大量的研究和开发,并且必须经过严格的测试以验证其潜在的好处。由于这些不确定性和基础设施的复杂性,基于格的 Merkle 树可能在短期内无法作为一个可行的选择,可能会延迟以太坊朝着可验证性目标的进展。
执行:EVM 执行的有效性证明
到目前为止,我们讨论的所有内容都集中在去除验证者需要存储先前状态的需求,这些状态用于从一个状态过渡到下一个状态。目标是创建一个更加去中心化的环境,在这个环境中,验证者可以在不维护数 TB 状态数据的情况下执行其职责。即便有了我们提到的解决方案,验证者仍然不需要存储整个状态,因为他们将通过区块中附带的见证数据接收到执行所需的所有数据。然而,为了过渡到下一个状态——并由此验证区块顶部的 stateRoot——验证者仍然必须自己执行 STF。这一要求再次对以太坊的许可性和去中心化性提出了挑战。
最初,The Verge 被设想为一个里程碑,专注于将以太坊的状态树从 Merkle 树过渡到 Verkle 树,以提高状态的可验证性。然而,随着时间的推移,它已经演变成一个更广泛的计划,旨在增强状态转换和共识的可验证性。在一个状态、执行和共识三者都能完全验证的世界中,以太坊的验证者将能够在几乎任何具有互联网连接的设备上运行,并且这些设备可以被归类为轻客户端。这将使以太坊更接近实现其“真正去中心化”的愿景。
问题定义
正如我们之前提到的,验证者每 12 秒执行一次名为 STF(状态转移函数)的函数。该函数以前一个状态和一个区块作为输入,生成下一个状态作为输出。每当一个新区块被提议时,验证者必须执行这个函数,并验证区块顶部代表状态的哈希(通常称为 stateRoot)是否正确。
成为验证者的高系统要求,主要来自于高效执行这一过程的需求。
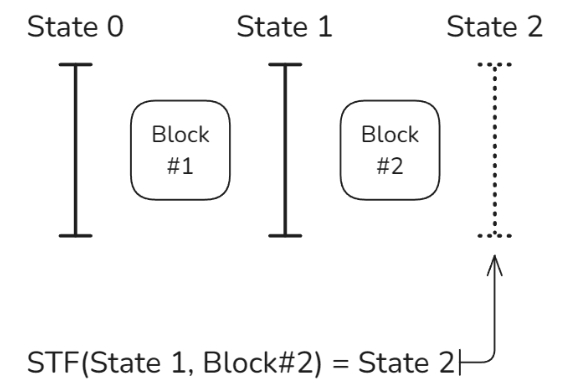
让智能冰箱成为以太坊验证者:面临的挑战与解决方案
如果你想让一个智能冰箱——没错,就是冰箱——变成一个以太坊验证者,并借助一些安装的软件来实现,你将面临两个主要障碍:
网速问题:你的冰箱很可能没有足够快的互联网连接,这意味着即使有我们前面讨论过的状态可验证性解决方案,它也无法下载执行所需的数据和证明。
计算能力不足:即便冰箱能够访问 STF 所需的数据,它也缺乏执行从头到尾的计算能力,或者构建新的状态树所需的计算资源。
解决方案:The Verge 提出的方案
为了解决 Light Clients 无法访问前一个状态或完整的最新区块数据的问题,The Verge 提出了一个方案:由提议者执行状态转移(STF),然后将证明附加到区块中。这个证明将包括从前一个状态根到下一个状态根的过渡,以及区块的哈希。通过这种方式,Light Clients 只需使用三个 32 字节的哈希值就能验证状态转移,而不需要 zk-证明。
然而,由于这个证明是通过哈希实现的,不能简单地说它仅验证状态转移。相反,附加到区块中的证明必须同时验证多个方面:
前一区块的状态根 = S,下一区块的状态根 = S + 1
区块哈希 = H
具体验证内容
区块本身的有效性:区块本身必须是有效的,同时其中的状态证明——无论是 Verkle 证明还是 STARK 证明——必须准确验证与区块相关的数据。
状态转移的验证:当 STF 使用执行所需的数据,并在对应于 H 的区块中执行时,状态中应该改变的数据必须正确更新。
树的构建过程验证:当用正确更新的数据重建新的状态树时,其根值必须与 S + 1 相符。
证明者与验证者的平衡
在前面提到的 Prover-Verifier 比喻中,通常来说,证明者和验证者之间会有一定的计算平衡。虽然生成证明所需要的多重验证机制为验证者提供了巨大的优势,但这也意味着生成这些证明以确保执行正确性,对于证明者来说会相对具有挑战性。目前,以太坊的区块需要在 4 秒内证明。然而,即使是我们今天最快的 EVM 证明者,也只能在大约 15 秒内证明一个平均区块【1】。
三种解决路径
为了克服这一主要挑战,有三条不同的路径可以选择:
证明并行化与聚合:ZK-证明的一个显著优势是它们可以进行聚合。将多个证明合并为一个紧凑的证明,显著提高了处理效率。这不仅减轻了网络负载,还加速了去中心化环境下的验证过程。对于像以太坊这样的庞大网络来说,它能够更高效地为每个区块生成证明。
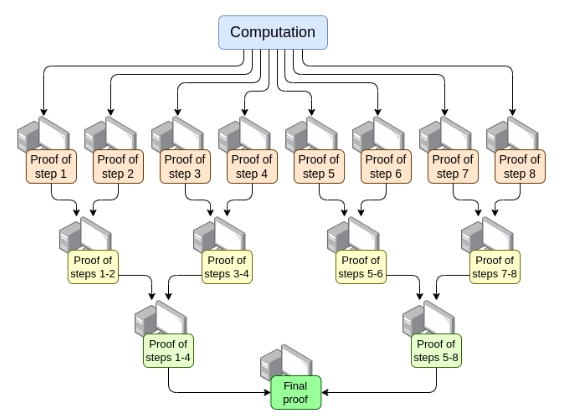
在生成证明的过程中,执行过程中的每个小步骤(例如计算步骤或数据访问)都可以单独进行证明,这些证明随后可以聚合成一个单一的结构。通过正确的机制,这种方法使得区块的证明可以由许多不同的来源(例如数百个 GPU)快速生成并去中心化地处理。这不仅提高了性能,同时也有助于去中心化目标的实现,通过吸引更多的参与者。
使用优化的证明系统
新一代的证明系统有潜力使以太坊的计算过程更快速、更高效。像 Orion、Binius 和 GKR 这样的先进系统可以显著减少通用计算的证明时间。这些系统旨在克服当前技术的局限性,提高处理速度并消耗更少的资源。对于一个以可扩展性和效率为核心的网络来说,类似的优化提供了巨大的优势。然而,完全实现这些新系统需要在生态系统内进行广泛的测试和兼容性努力。
Gas费用的变化
在以太坊虚拟机(EVM)上执行操作时,历史上Gas费用通常是基于计算成本来决定的。然而,现在,另一个指标开始变得更为重要:证明复杂性。尽管某些操作相对容易证明,但其他操作则结构更为复杂,需要更长时间才能验证。根据操作的计算工作量和证明难度来调整Gas费用,对于提高网络的安全性和效率至关重要。
这种方法能够最小化最坏情况和平均情况之间的差距,从而实现更加一致的性能。例如,较难证明的操作可能需要更高的Gas费用,而较容易证明的操作则可以降低费用。此外,用适应 STARK 的替代数据结构(如状态树或交易列表)替代以太坊现有的数据结构,还可以进一步加速证明过程。这些变化将有助于以太坊实现其可扩展性和安全性目标,同时使其可验证性的愿景更为现实。
以太坊推动执行证明的努力代表了实现其可验证性目标的重要机会。然而,达成这一目标不仅需要技术创新,还需要增加工程方面的努力,并做出社区内部的关键决策。在 Layer 1 上使执行过程可验证,必须在确保广泛用户群体可访问的同时,保持去中心化并与现有基础设施保持一致。建立这种平衡增加了在执行过程中证明操作的方式的复杂性,这凸显了诸如并行证明生成等技术进展的必要性。此外,这些技术的基础设施要求(例如查找表)必须实现并投入使用,这仍然需要大量的研究和开发工作。
另一方面,专用电路(如 ASIC、FPGA、GPU)专门为某些任务设计,具有显著加速证明生成过程的潜力。这些解决方案比传统硬件提供更高的效率,并且能够加速执行过程。然而,以太坊在 Layer 1 级别的去中心化目标使得这些硬件不应仅仅对少数几方可用。因此,这些解决方案预计将在 Layer 2 系统中得到更广泛的应用。然而,社区也需要就证明生成的硬件要求达成共识。一大设计问题是:证明生成是否应该在像高端笔记本电脑这样的消费级硬件上进行,还是需要工业级基础设施?这一问题的答案将决定以太坊的整体架构——即在 Layer 2 解决方案上进行激进的优化,同时在 Layer 1 上采取更为保守的方式。
最后,执行证明的实现直接关系到以太坊其他路线图目标的实现。引入有效性证明不仅支持 无状态化 等概念,还通过使单独质押等领域更具可访问性,增强以太坊的去中心化目标。目标是使得即使是最低规格的设备也能参与质押。此外,基于计算难度和可证明性的重构 EVM 的Gas费用,可以缩小平均情况和最坏情况之间的差距。然而,这种变化可能会打破与当前系统的向后兼容性,并迫使开发者重写代码。因此,执行证明的实施不仅是一个技术挑战——它是一个必须设计来保持以太坊长期价值的过程。
最后一步:实现完全可验证性的共识机制
以太坊的共识机制致力于在保持去中心化和可访问性的同时,实现可验证性的目标。在这个框架下,概率共识和确定性共识方法各有不同的优势和挑战。
概率共识
概率共识基于一种传播式的通信模型。在这种模型中,节点并不会直接与代表网络的所有节点通信,而是与随机选择的一组64或128个节点共享信息。节点的链选择基于这些有限的信息,这就引入了错误的可能性。然而,随着区块链的推进,这些选择预计会逐渐收敛到正确的链上,错误率最终接近0%。
概率共识结构的一个优势是,每个节点并不会将自己的链视图作为单独的信息进行广播,从而减少了通信开销。因此,这种结构能够支持更多的、权限开放的去中心化节点,并且系统要求较低。
确定性共识
与概率共识不同,确定性共识通过“一对多”的通信模型来运作。在这种模型中,节点将其链视图作为投票发送给其他所有节点。这种方法会产生更高的消息密度,随着节点数量的增长,系统可能最终达到其限制。然而,确定性共识的最大优势在于具体的投票机制,使得可以准确知道哪些节点投票支持了哪个分叉。这确保了链的快速和确定性最终性,保证了区块的顺序无法改变,并使其可验证。
以太坊的共识机制平衡
为了在保持去中心化和开放结构的同时提供可验证的共识机制,以太坊在 插槽 和 纪元(Epochs)之间达成了一种平衡。
插槽(Slot):插槽是每12秒一个时间间隔,在该时间间隔内,验证者负责生成一个区块。尽管在插槽级别使用的概率共识让区块链能够更灵活、去中心化地运行,但在确定顺序和可验证性方面仍然存在一些局限性。
纪元(Epoch):一个纪元由32个插槽组成,在这个层次上,验证者投票决定最终区块链的顺序,确保了链的确定性并使其可验证。然而,尽管这个确定性结构在纪元级别通过具体的投票提供了可验证性,它由于概率结构的存在,无法在纪元内部提供完全的可验证性。
Sync Committee:加强纪元内的可验证性
为了弥补这一差距并增强纪元内的概率结构,以太坊开发了解决方案——同步委员会(Sync Committee)。同步委员会旨在提高概率共识在纪元内的可验证性,确保区块的最终确定性和顺序不受影响,同时维持去中心化和开放性。
通过将概率共识和确定性共识相结合,并通过同步委员会来进一步增强纪元内的验证能力,以太坊在实现去中心化的同时,确保了其可扩展性和可验证性的目标。这种混合共识机制为以太坊的长期可持续性和去中心化打下了坚实的基础,并为网络上的参与者提供了更高的安全性和灵活性。
共识的零知识证明化
The Verge旨在通过采用零知识证明技术(zk-proof)增强以太坊当前和未来的共识机制,而不是完全替代它们。此举旨在在保留去中心化和安全性核心原则的同时,现代化以太坊的共识流程。通过零知识技术优化以太坊链的所有历史和当前共识过程,对实现以太坊长期可扩展性和效率目标至关重要。以太坊共识层使用的基本操作在这一技术转型中发挥着重要作用。接下来,让我们更深入地探讨这些操作及其所面临的挑战。
ECADD 操作:
目的:该操作用于聚合验证者的公钥,对于确保链的准确性和高效性至关重要。得益于BLS签名的可聚合特性,多个签名可以合并为一个结构,这减少了通信开销,使链上的验证过程更加高效。有效地确保大型验证者群体的同步,使得这一操作显得尤为关键。
挑战:如前所述,以太坊的验证者在纪元期间对链的顺序进行投票。如今,以太坊网络大约有110万个验证者。如果所有验证者试图同时传播他们的投票,将会对网络造成极大压力。为了避免这种情况,以太坊允许验证者在每个纪元内按槽位投票,每个槽位仅有1/32的验证者进行投票。尽管这种机制减少了网络通信的开销,并提高了共识效率,但鉴于目前的验证者数量,每个槽位大约有34,000个验证者进行投票,这意味着每个槽位大约需要进行34,000次ECADD操作。
配对操作(Pairings):
目的:配对操作用于验证BLS签名,确保链上纪元的有效性。该操作允许批量验证签名,但它不支持zk-friendly(零知识证明友好),使得使用zk-proof技术进行证明时非常昂贵。这在创建集成的零知识验证流程时构成了一个主要挑战。
挑战:以太坊中的配对操作每个槽位最多限于128个认证(聚合签名),因此相较于ECADD操作,配对操作的数量较少。然而,这些操作不支持zk-proof,导致它们在zk-proof系统中的成本极高。证明一个配对操作的零知识证明比证明一个ECADD操作的成本要高出数千倍。这使得配对操作在零知识技术中的适配成为以太坊共识验证流程中最大的障碍之一。
SHA256 哈希函数:
目的:SHA256哈希函数用于读取和更新链的状态,确保链数据的完整性。然而,它们不支持zk-proof,这导致在基于零知识证明的验证过程中效率低下,成为以太坊未来可验证性目标的主要障碍。
挑战:SHA256哈希函数经常用于读取和更新链的状态。然而,它们的zk-unfriendliness(不支持零知识证明)与以太坊基于zk-proof的验证目标相冲突。例如,在两个纪元之间,每个验证者都需要运行以太坊共识层的状态转换函数(STF)来更新状态,计算奖励和惩罚,这基于验证者在该纪元内的表现。此过程严重依赖SHA256哈希函数,极大地增加了基于zk-proof系统的成本。这为将以太坊的共识机制与zk技术对接,提供了巨大的挑战。
当前共识层使用的ECADD、配对和SHA256操作在以太坊的可验证性目标中扮演着关键角色。然而,它们的zk-unfriendliness(不支持零知识证明)在实现这些目标的过程中带来了显著挑战。ECADD操作由于验证者投票量庞大,给网络带来了昂贵的负担,而配对操作虽然数量较少,但使用zk-proof证明时却比ECADD操作贵数千倍。此外,SHA256哈希函数的不支持zk-proof使得证明信标链的状态转换变得异常困难。这些问题凸显了以太坊需要进行全面转型,以将现有基础设施与零知识技术对接。
解决方案“Beam Chain”:重新构想以太坊的共识层
2024年11月12日,Justin Drake在Devcon的演讲中提出了一个名为“Beam Chain”的提案,旨在从根本上和全面地改造以太坊的共识层。信标链(Beacon Chain)已经在以太坊网络的核心运行近五年。然而,在此期间,信标链没有经历任何重大的结构性变化。与此相对的是,技术进展迅速,远远超过了信标链的静态特性。
在演讲中,Justin Drake强调,以太坊在过去五年中在多个关键领域获得了重要的经验教训,包括MEV(最大化可提取价值)理解、SNARK(简洁非交互式论证)技术的突破以及对过去技术错误的回顾性认知。基于这些新收获的知识,设计方案被归纳为三个主要支柱:区块生产、质押和加密学。以下图表总结了这些设计和提案的路线图:
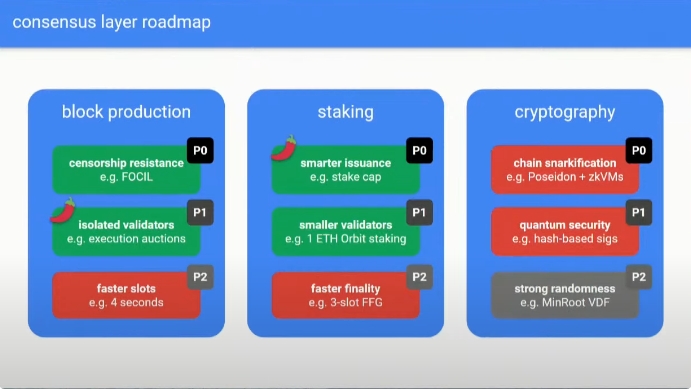
绿色和灰色框表示逐步实施的渐进性发展,可以每年逐一实现。这些改进类似于之前的升级,可以逐步集成而不干扰以太坊现有的架构。
另一方面,红色框表示高协同效应、大规模和基础性的变革,必须一起实施。根据Drake的说法,这些变化旨在通过一次重大的飞跃提升以太坊的能力和可验证性。
在本节中,我们详细讨论了The Verge的共识、状态和执行步骤,其中一个突出的问题是以太坊信标链中使用的SHA256哈希函数。虽然SHA256在确保网络安全和处理交易方面发挥着核心作用,但其缺乏对zk技术友好的特性,成为实现以太坊可验证性目标的重大障碍。其高计算成本和与zk技术的不兼容性,使其成为必须在未来以太坊发展中解决的关键问题。
Justin Drake在Devcon演讲中提出的路线图设想用zk友好的哈希函数(如Poseidon)取代信标链中的SHA256。该提案旨在使以太坊的共识层现代化,使其更具可验证性、更高效,并与zk-proof技术对接。
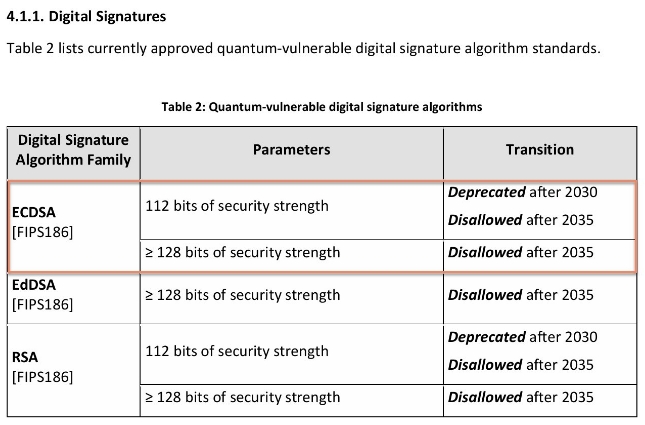
在这种背景下,我们看到以太坊不仅面临着与zk不友好哈希函数相关的挑战,还需要重新评估其共识层中使用的数字签名,以确保长期的安全性。随着量子计算的发展,目前使用的数字签名算法(如ECDSA)可能面临重大威胁。正如NIST发布的指南所指出,具有112位安全级别的ECDSA变种将在2030年逐步淘汰,并于2035年完全禁用。这迫使以太坊和类似网络必须朝着更加具有抗量子能力的替代方案过渡,例如量子安全的签名。
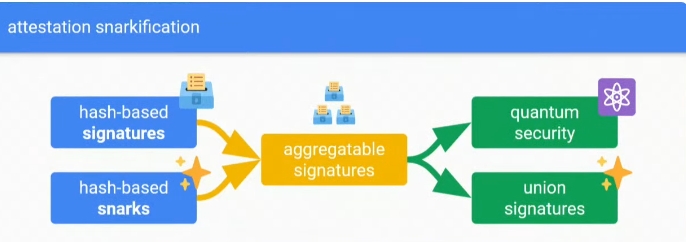
此时,基于哈希的签名作为抗量子解决方案浮现,它们将在支持网络的安全性和可验证性目标方面发挥关键作用。解决这一问题还消除了使信标链可验证的第二大障碍:BLS签名。以太坊在确保量子安全方面可以采取的最重要步骤之一是采用后量子解决方案,如基于哈希的签名和基于哈希的SNARKs。
正如Justin Drake在Devcon演讲中强调的,哈希函数由于依赖于预像抗性,本质上是抗量子计算的,使它们成为现代密码学的基础构件之一。这一特性确保即使是量子计算机也无法有效地从给定的哈希值反推原始输入,从而保持其安全性。基于哈希的签名系统允许验证者和见证者仅基于哈希函数生成签名,确保后量子安全性,同时提供更高的网络可验证性——尤其是在使用SNARK友好的哈希函数时。这种方法不仅提升了网络的安全性,还使以太坊的长期安全基础设施变得更加稳健,具备未来-proof能力。
这个系统依赖于将基于哈希的签名和基于哈希的SNARK(类似STARK的证明)结合,创建可聚合的签名方案。可聚合签名将成千上万的签名压缩为一个结构,将其减少到仅几百千字节的证明。这种压缩显著减少了网络上的数据负载,同时大大加速了验证过程。例如,以太坊中为一个单一槽产生的成千上万的验证者签名可以通过一个聚合签名来表示,从而节省存储空间和计算能力。
然而,这个方案最显著的特点是它的无限递归聚合。也就是说,一组签名可以在另一组签名下进一步结合,并且这一过程可以在链上继续进行。借助这一机制,并考虑到未来的技术进展,可以公平地说,这为目前BLS无法实现的可能性打开了大门。
最终思考与结论
以太坊的可验证性之路代表了区块链技术的根本转变。The Verge倡议通过使用Verkle树进行状态验证以及使用STARK证明进行可扩展过渡,解决了核心的低效问题。
其中最雄心勃勃的提案之一是Beam Chain,这是一项对以太坊共识层的全面重设计。通过解决信标链的局限性,并引入zk友好的替代方案,这一方法旨在提升以太坊的可扩展性,同时保持其去中心化和可访问性的核心原则。然而,这一过渡也凸显了以太坊在平衡计算需求与保持一个无需许可、包容性网络的目标时所面临的挑战。
随着NIST计划到2035年淘汰当前的椭圆曲线加密算法,以太坊必须采纳像基于哈希的签名和Poseidon这样的抗量子解决方案。这些解决方案也有其效率上的权衡。
STARKs在以太坊路线图中的使用进一步强调了可扩展性和可验证性。虽然它们在提供透明且抗量子的证明方面表现出色,但它们的整合带来了与证明方计算成本和小数据效率相关的挑战。必须解决这些难题,才能充分实现以太坊的无状态化和高效块验证愿景,确保网络在需求日益增长的情况下依然保持稳健。
尽管有这些进展,仍然存在一些关键挑战。以太坊必须应对zk友好性、共识可扩展性和整合抗量子加密技术的复杂性问题。此外,现有基础设施的向后兼容性也提出了实际障碍,这需要精心的工程解决方案,以防止对开发者和用户造成干扰。
让以太坊与众不同的,不仅仅是它的技术创新,还有它解决区块链难题的渐进方法。未来的道路——无论是通过Beam Chain、Verkle树还是STARK证明——都依赖于开发者、研究人员和更广泛社区的合作努力。这些进展不是一蹴而就的,而是为创建一个透明、去中心化和可验证的互联网奠定基础。
以太坊的演变凸显了它在塑造Web3时代中的关键角色。通过用实际的解决方案应对当今的挑战,以太坊正朝着一个可验证性、抗量子性和可扩展性成为标准而非例外的未来迈进。
声明:本网站所有相关资料如有侵权请联系站长删除,资料仅供用户学习及研究之用,不构成任何投资建议!