LAMMbert：由Lambert W函数定义的自动做市商

2024-01-07 10:03:02 114

引子

AMM（Automated Market Maker）自动做市商，作为一种去中心化金融协议，通过智能合约和算法来执行交易和确定价格。目前常见的算法是来自 Uniswap 的“常量曲线”（CSMM & CPMM）。除此之外，还有 Curve Finance 提出的“稳定交易曲线”（StableSwap curve），它混合了常和 (CS) 和常积 (CP) 方程，以适应不同价格波动的市场情况。最近，一种由 Lambert W 函数定义的集中流动性 AMM被提出，它用 LW 函数达到了混合 CS 与 CP 的效果，有望减少计算复杂性与资源损耗，提高流动池交易体验。

本文为 LAMMbert 英文文档的中文翻译，原文 pdf 地址：https://github.com/euler-mab/LAMMbert/blob/main/LAMMbert.pdf，作者为 Michael Bentley，在阅读本翻译同时，可以随时参考原文以获取更多详细信息。

简介

两种流行的自动做市商（AMM）是常和（CSMM）和恒乘（CPMM）做市商。CSMM 的简单版本由以下方程式定义

这个方程以一种有趣的方式将 CSMM 和 CPMM 方程结合在一起，类似于 StableSwap（Michael Egorov. “Stableswap-efficient mechanism for stablecoin liquidity[1]”. In: (2019).）。当 c = 0 时，我们得到一个纯 CPMM 方程，当 c 增大时，它趋向于一个纯 CSMM 方程。

我们现在证明方程（5）可以通过使用 Lambert W 函数来求解。两边取指数，然后乘以 c，并重新排列，我们得到

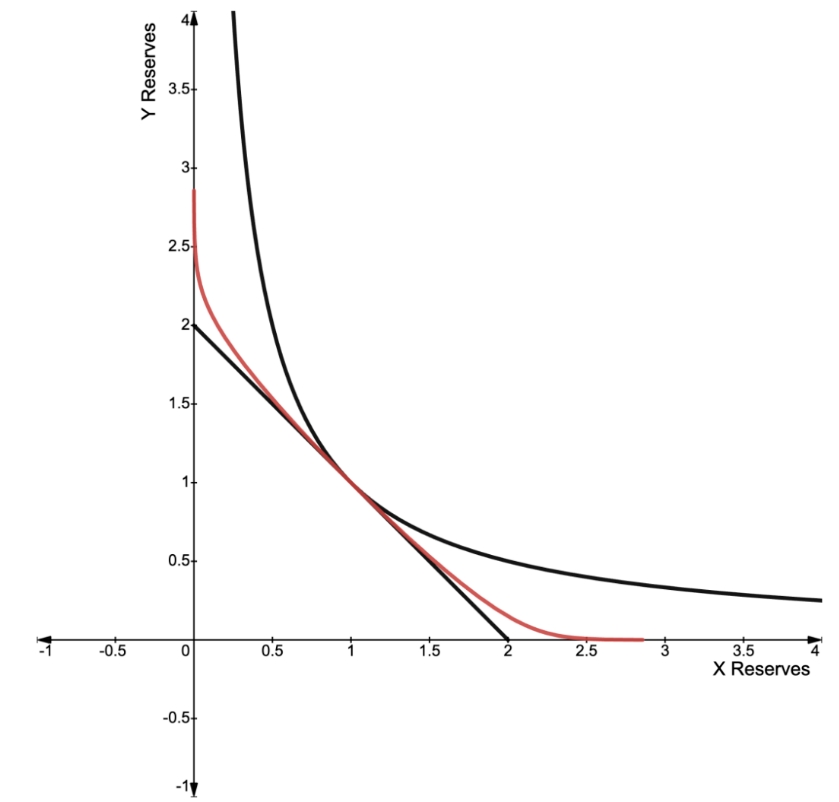
图1：LAMMbert 自动做市商。常和与常乘做市商可以结合，得到一个依赖于集中参数的中间曲线。该曲线可以明确地用 Lambert W 函数来定义。

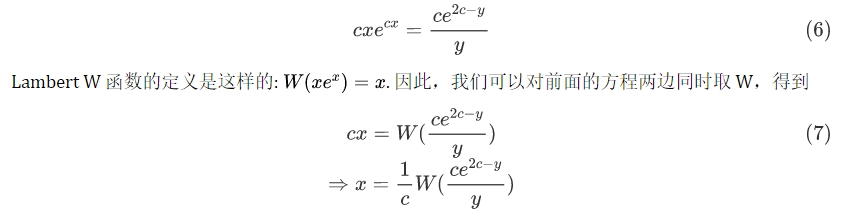
因此，方程(6)可以用 Lambert W 函数的明确形式来表示。我们将其称为 LAMMbert AMM。图1 显示了其双币模型的图形。这种形式的方程出现在线性恒定系数时滞方程的求解中（参见 Robert M Corless 等人的文章“On the Lambert W function[3]”。In: Advances in Computational Mathematics 5 (1996), pp. 329–359），尽管那些方程和自动做市商之间的关系还不清楚，如果有的话。

需要注意的是，目前还没有经过审计的方法可以在链上使用 Lambert W 函数，因此目前尚不清楚是否可以在智能合约中实现 LAMMbert。然而，最近有一个提议，即将将这样的函数添加到 solady[4] 存储库中，这可能会在不久的将来改变这种情况。

附录

欢迎大家加入对 LAMMbert 的讨论，这个讨论可以在 twitter 上找到：

https://twitter.com/euler_mab/status/1724403149593583745

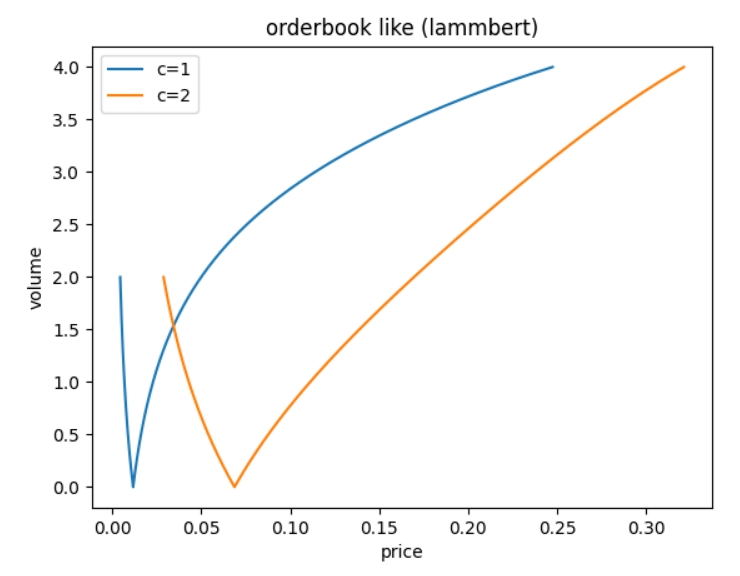
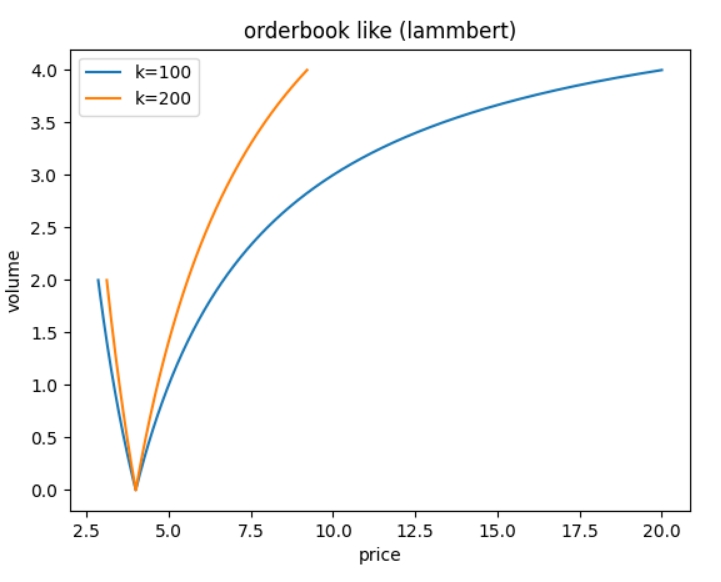
我们绘制了使用常积曲线（uni v2使用）与 LAMMbert 曲线模拟的订单簿情况：