Manta Pacific 是 Manta Network 推出的、为 ZK 应用设计的以太坊模块化 Layer2，目前已获得 Polychain、Binance labs、CoinFund、SevenX Ventures 等机构超 6000万美元融资。

Manta 将 ZK 电路内置到 Manta Pacific Layer2，设计极其模块化，相当于为 DApp 提供了多个 ZK 功能模块。开发者仅需几行代码，通过 SDK、API 便可调用 ZK 功能。

并且，在 Layer2 内完成 ZK 证明的生成和验证，可让 Manta Pacific 生态应用完整地实现 ZK 功能，可将 ZK 的正确性、压缩交易的简洁性等特性，完整地与现有应用结合，或让开发者根据 ZK 特性部署新应用，这是目前 Manta Pacific 独有的。

零知识证明概念可以扩展到任何 NP 问题。零知识证明系统从理论上发展到实际应用，已经成为密码学研究中的热点。

Manta 所用的主要密码学原语是一种特殊类型的非交互式零知识证明，称为公开可验证的零知识简洁非交互证明（zkSNARK）。简单来说，就是一个能够让人验证一个复杂计算的结果而无需重复整个计算的系统。

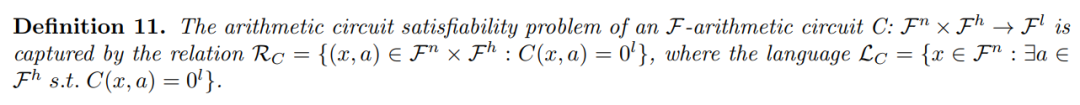
具体来说，对于一个有限域（ Finite Field） F 上的算术电路（arithmetic circuit） C，输入、输出和中间值都在 F 中。

我们考虑一个输入为 x 属于 Fn 和一个辅助输入 a 属于 Fh 的电路，我们称 a 为证人(witness)。一个电路满足性问题就是给定x，存在一个输入a，使得电路 C 的输出为 0，即C(x,a) = 0。

零知识证明的满足性是通过三个多项式时间算法定义的：KeyGen、Prove、Verify。

KeyGen(1^λ, C) -> (pk, vk)。在安全参数λ（例如128比特）和算术电路 C 的情况下，KeyGen 算法会随机生成一个证明密钥 pk 和验证密钥 vk。这两个密钥是公开的，可以被用来无限次地证明/验证电路 C 的成员资格。

Prove(pk, x, a) -> π。使用证明密钥 pk 和任何(x, a)作为输入，证明者 Prove 输出一个非交互式的证明 π 来声明 x 属于 L_C，即C(x,a)=0。

Verify(vk, x, π) -> {0,1}。验证者 Verify 使用验证密钥 vk、x 和证明 π 作为输入，如果 x 属于 L_C，则输出1；否则输出0。

零知识证明就像是一场魔术表演。Alice 通过一系列巧妙的手法（这里指数学计算），向 Bob 展示了一些线索（这里指证明），这些线索足以让 Bob 相信箱子里确实有秘密，让他确信 Alice 不是在撒谎。

在这个过程中，Alice 使用了一把特殊的“魔法钥匙”（这里指公开的验证密钥vk），任何人都可以用这把钥匙来验证线索。这个“魔术表演”可以在不同的地方和不同的人前反复进行。

除了zkSNARKs之外，Manta 还用到：

非交互式承诺方案（COMM）：这是一种非交互式的承诺机制，确保信息的一致性。简单地说，你可以将某个信息和一个随机数一起“锁”在一个承诺里，这个承诺可以向别人证明你确实提交了某些信息。而 Binding 约束 意味着一旦一个承诺被作出，就不可能更改其内容。例如，给定一个随机种子 r 和消息 m，承诺是 c := COMMIT_r(m)，可以通过揭示 r 和 m 来验证这个承诺。

伪随机函数（PRF）：这是一种可以从一个固定的输入生成看似随机的输出的函数。在密码学中，我们通常会用标签来区分不同的伪随机函数，这样即使它们基于相同的核心函数，也能生成不同的输出。这些函数可以用来生成地址、空号（一种用于加密货币的随机数）和公钥。

密码学累加器（Cryptographic Accumulators）：它是一种支持高效、零知识和成员身份证明的工具。简而言之，累加器允许你将大量的信息“累加”到一个小的、固定大小的值中，并且可以对这些信息的存在进行高效验证，而不需要提供完整的信息。在区块链中，累加器可以用来改善数据存储和验证过程。

集成加密方案（ECIES）：这是建立在椭圆曲线 Diffie-Hellman 密钥交换之上的加密方案。简单来说，它允许两个交互方在不安全的通道上安全地交换信息。发送方使用接收方的公钥将信息加密，而只有拥有对应私钥的接收方才能解密这个信息。这种方案通常和 AES 这样的块密码器一起使用，以提供强大的加密保护。

使用 Manta ZK 电路交易，遵循 UTXO 模型。需特别注意的是，这里的交易，指的是在 Manta Pacific 排序器向 Layer1 提交交易前，在自身 Layer2 内部，由零知识证明参与方（证明者和验证者）完成的交易验证、ZK 证明生成。

正常 DApp 遵循通常 EVM 交易规则，只有当 DApp 调用 ZK 电路，将 ZK 与自己的 DApp 结合时，才会遵循以下交易模型。

Manta ZK 电路内操作，如交易，遵循 UTXO（未花费交易）模型，从一个或多个输入消费旧币并生成新币。特别是，铸币操作会生成新的 UTXO，而交易操作则消费这些 UTXOs。

在 Manta 电路转账过程中，Alice 想要将她的代币 CoinA 和 CoinB 转移到新地址。在这个系统中，每个代币都会有一个承诺 Commitment，这相当于是代币存在的证明，并且包含了代币的某些属性。

每个代币有一个唯一的序号，这个序号在转账时会被曝光，表示旧的代币已经作废。为了确保交易的合法性，这个过程会包含一个零知识证明，用来验证交易的有效性。

Manta 系统会验证这个零知识证明，确保交易中的新代币 CoinA 和 CoinB 交易涉及的序号是首次使用。

兑换过程与转账类似，但主要区别在于输出代币的类型可能不同。Alice 可能想要将她的一种代币兑换为另一种，系统会验证这次兑换是否保持了总金额不变。

该模型遵循以下算法步骤：

Setup: 系统的初始化阶段，设定 NIZK 系统参数。

GenMint: 用户生成一个铸币交易，选择一个 UTXO 作为输入，并指定新币的面值和接收者。该过程生成一个包含零知识证明的铸币交易。

Mint: 该交易由网络验证，并在成功验证后将新的 UTXO 记录在区块链上。

GenTransfer: 用户生成转账交易，这需要提供当前的账本状态、要转移的代币、接收者的公钥等信息，并生成一个包含零知识证明的转账交易。

Transfer: 验证器执行转账交易并在成功后更新账本状态。

GenReclaim: 用户生成回收交易，以便回收未完全使用的 UTXO 中的余额。

Reclaim: 验证器执行回收交易并在成功后更新账本状态。

Manta 使用 ZK 提出了一个复杂的安全性证明框架，主要针对一种 zkSNARK方案。目的是为了确保交易的安全性，防止双重支付和其他潜在的安全风险。

模拟器（Sim）构造：为了展示 zkSNARK 方案的零知识属性，构建了一个模拟器，该模拟器能够生成与 Real adv 不可区分的 View。这是通过上述声明的定理证明的，该定理显示了在给定的 COMMIT 方案和 PRF 条件下，无法区分来自 Real Adv 和 Ideal adv（由模拟器构造）的 View，因为两者的区分度是可忽略的。

混合论证：通过逐步替换 Real adv 的 View 中的元素，构建了一系列的中间 View，直到最终达到 Ideal View。这一系列中间 View 的构建基于一个重要的前提，即任何能够区分两个连续中间 View 的 adversary 敌手，同样也能够区分最初的Real adv View 和最终的 Ideal adv View。证明展示了任何能区分这些 View 的敌手的优势是多项式级别的，这表明了 zkSNARK 方案的安全性。

面对不同类型交易（如转账交易和 Claim）时，构造特定对手以挑战 COMMIT 方案的属性或 zkSNARK 方案的零知识属性。如果存在这样的对手，将会违反初始的假设，由此证明了 Manta 协议的安全性。

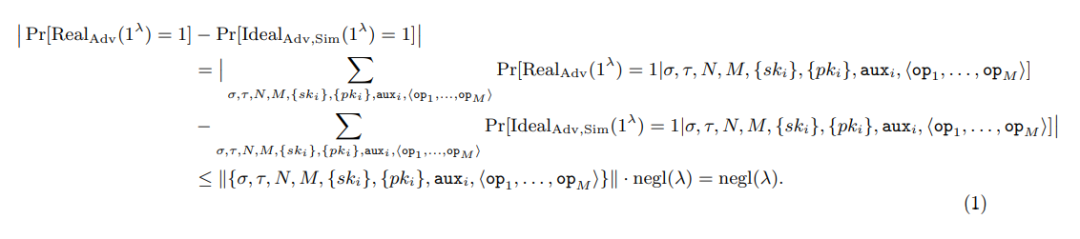
事实上，对于这些系统的安全性证明，通常会包括构造两个实验：一个实际的协议运行（Real）和一个理想的协议运行（Ideal），其中模拟器（Sim）模拟真实的对手行为。如果没有有效的方式可以区分这两个实验的输出，那么我们可以说协议是安全的。

Ideal /Real 安全性模型是零知识证明中的一个常见概念，用于证明协议在面对潜在的攻击者时保持其安全性。在零知识证明系统中，重要的是验证者（或系统）能够确信某些陈述是正确的。

关于 Manta Pacific

Manta Network 致力于为零知识证明（ZK）应用提供模块化区块链支持。Manta Pacific 是面向 EVM 生态的 ZK 应用及 DApp 的模块化 Layer2 生态，通过 Manta 通用电路实现 ZK-as-a-Service，利用 Celestia 数据可用层提供模块化支持，为用户提供最低 Gas 成本和最好的用户体验。

Manta Network 由来自哈佛、麻省理工及 Algorand 等顶级院校和机构的资深创业者联合创建。Manta Network 获得包括 Binance Labs 和 Polychain Capital 在内的顶级 Web3 投资基金投资，通过参与 Alliance DAO 和伯克利 Berkeley Blockchain Xcelerator 等一流 Web3 加速器，不断发展。

声明：本网站所有相关资料如有侵权请联系站长删除，资料仅供用户学习及研究之用，不构成任何投资建议！