在上一课中，我们研究了密码学哈希函数及其攻击。密码学哈希函数几乎用于每一个保证完整性和认证的协议中。但在区块链环境中，它们最重要的应用之一是在默克尔树中。

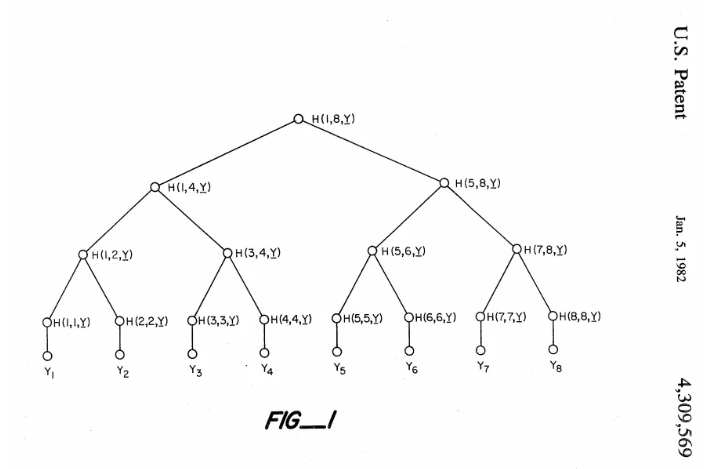
来自默克尔树的原始专利。

默克尔树由现代密码学的奠基人之一 Ralph Merkle 发明。尽管他在 1982 年为默克尔树申请了专利，但该专利早已过期。默克尔树广泛应用于许多领域，包括 Git、BitTorrent、ZFS、证书透明框架，当然还有几乎所有的加密货币。

让我们通过一个简单的例子来看看如何在应用程序中使用默克尔树。

构建默克尔树

假设我们正在设计一个文件共享协议。我们假设我们共享的文件很大——比如 Linux 发行版。

在这个协议中，一旦用户完成文件下载，他们需要以某种方式验证文件在传输过程中没有被损坏。TCP 本身可以纠正大多数随机错误，但即便如此， 处理这种大小的文件时[4]腐败错误仍然很常见。我们如何在应用层确保完整性？

这是一个想法：让我们在 Linux ISO 旁边附带一个密码学哈希。这样，当用户下载完 ISO 后，他们可以对其进行哈希并检查摘要是否匹配。哈希速度非常快——即使在单核上，你也可以每秒哈希数百兆字节。

Linux 发行版现在与其哈希一起发布。

但如果哈希不匹配怎么办？你怎么知道文件中的错误在哪里？

实际上，你无法知道错误在哪里。你必须丢弃所有的 2GB 并重新下载，希望这次不会发生损坏。这似乎是一个糟糕的解决方案。

这是一个想法：如果我们将数据分成块并为每个块附带哈希呢？

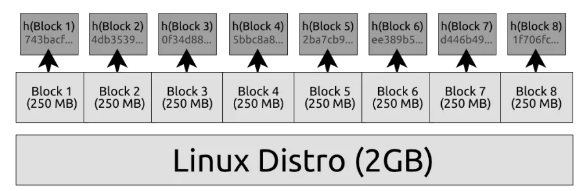
这很好！现在，如果我们的数据中有随机损坏，我们可以检查哪个 250MB 块被损坏，然后只重新下载那个块。缺点是我们需要在下载时附带所有 8 个哈希：

Block 1 digest: 743bacf85062c45f533060e3abb3dc1f02683269

Block 2 digest: 4db3539ecf02e69ffacec45751129e38bdfa469e

Block 3 digest: 0f34d88b134aece384b3d079996d08ee7eadecfd

Block 4 digest: 5bbc8a852490d2f9d9e0067f408950539af0bda9

Block 5 digest: 2ba7cb929bc68c6706b8be03946add92e941999d

Block 6 digest: ee389b56b4a6ff4407df5ffd5f675c2fa73edd22

Block 7 digest: d446b49425506732cfd707865908a99a1ab15ba7

Block 8 digest: 1f706fc900b2c4543525ea1434a201d169004a3d

对于 250MB 的块，这可能没问题，但如果我们想要更小的块以最小化损坏的影响，那么我们需要超过 8 个哈希。如果我们想要 128KB 的块，我们需要 15,000 个哈希，如果我们想要 8KB 的块，我们需要 250,000 个哈希。这很快就变得难以管理。

这时默克尔树就派上用场了。默克尔树是一种密码学累加器。密码学累加器允许你将任意多的数据压缩到固定的空间中。换句话说，默克尔树让我们可以表示任意多的块，同时只传输一个单一哈希。

默克尔树也被称为 _哈希树_，因为它们在树中向上哈希数据。用代码解释很简单——以下是如何用两个元素创建哈希树。

    from hashlib import sha1

    def h(s): return sha1(s.encode()).hexdigest() # 哈希辅助函数

    block1 = "Block 1"

    block2 = "Block 2"

    digest1 = h(block1)

    digest2 = h(block2)

    root = h(digest1 + digest2)

    print(root)

    # d1c6d4f28135f428927a1248d71984a937ee543e

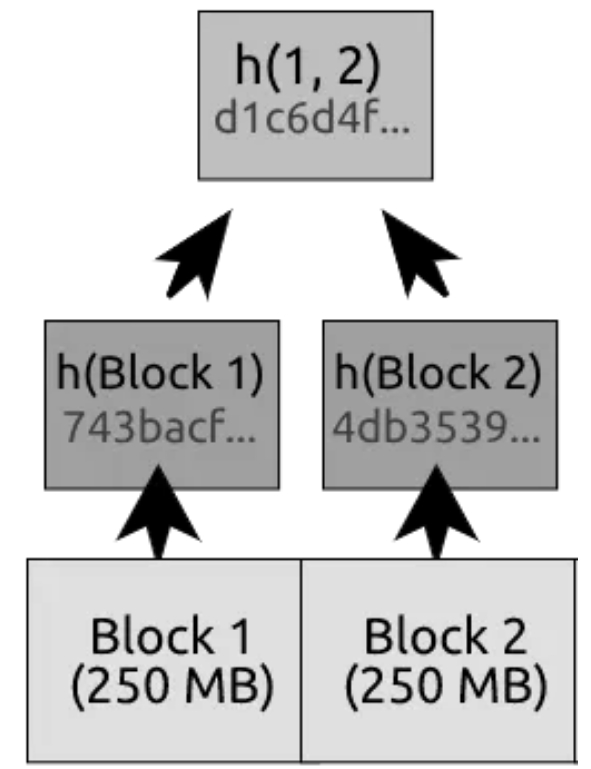
（此图使用 h(1, 2) 表示以提高可读性，但实际上是 h(h(1) + h(2))。）

通过连接两个摘要并对其进行哈希，哈希树的根就承诺了两个摘要。想一想：如果有其他方法可以生成相同的根，那就意味着存在哈希碰撞。对于强密码学哈希函数，哈希碰撞应该是不可能的。因此，这棵哈希树的根，称为默克尔根，必须是这个确切树的 唯一标识符。

（如果你不理解这个论点，请用代码再试试另一个例子！这种直觉非常重要，我们将继续在此基础上构建。）

因此，默克尔根是对所有原始数据的累加器，这些数据被哈希以生成这棵树。它还按_顺序_承诺这些数据，因为我们使用字符串连接在底层块上组合它们的值。（如果你使用了像加法或异或这样的交换操作而不是连接，那么技术上你可以交换某些块的顺序并得到相同的根。这是不理想的，所以不要犯这个错误。）

那么这如何扩展到许多块呢？很简单。我们在数据层上重复相同的操作，直到得到一个根。

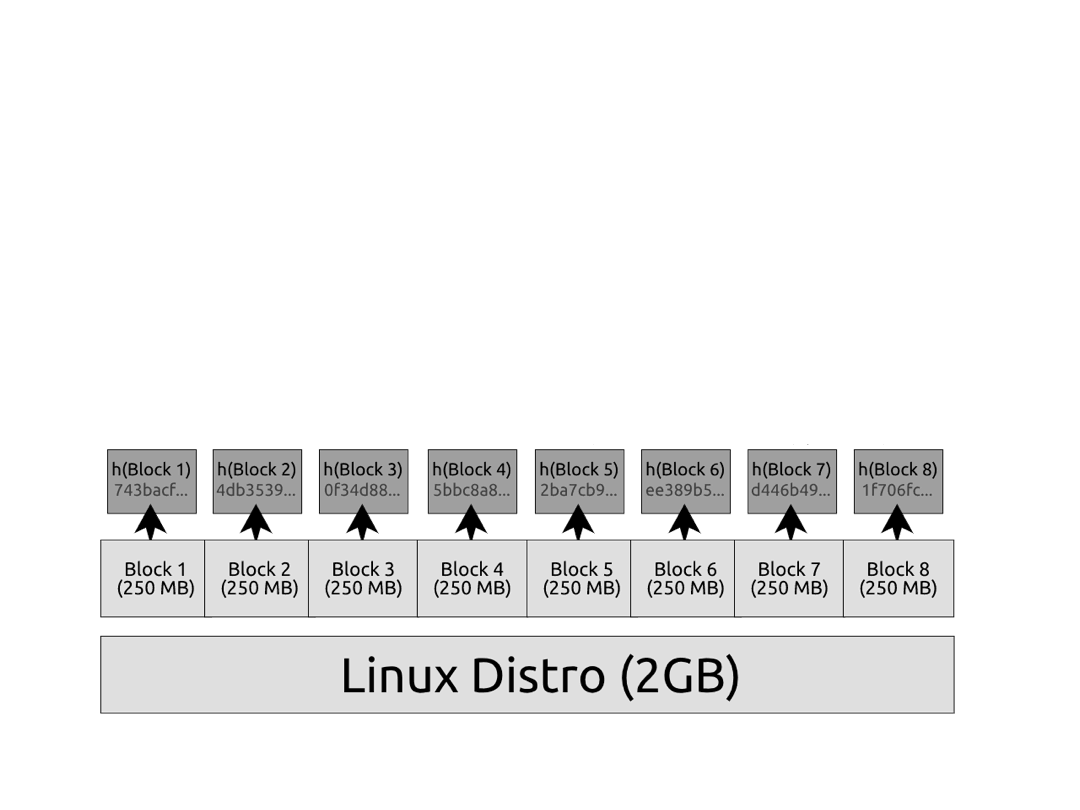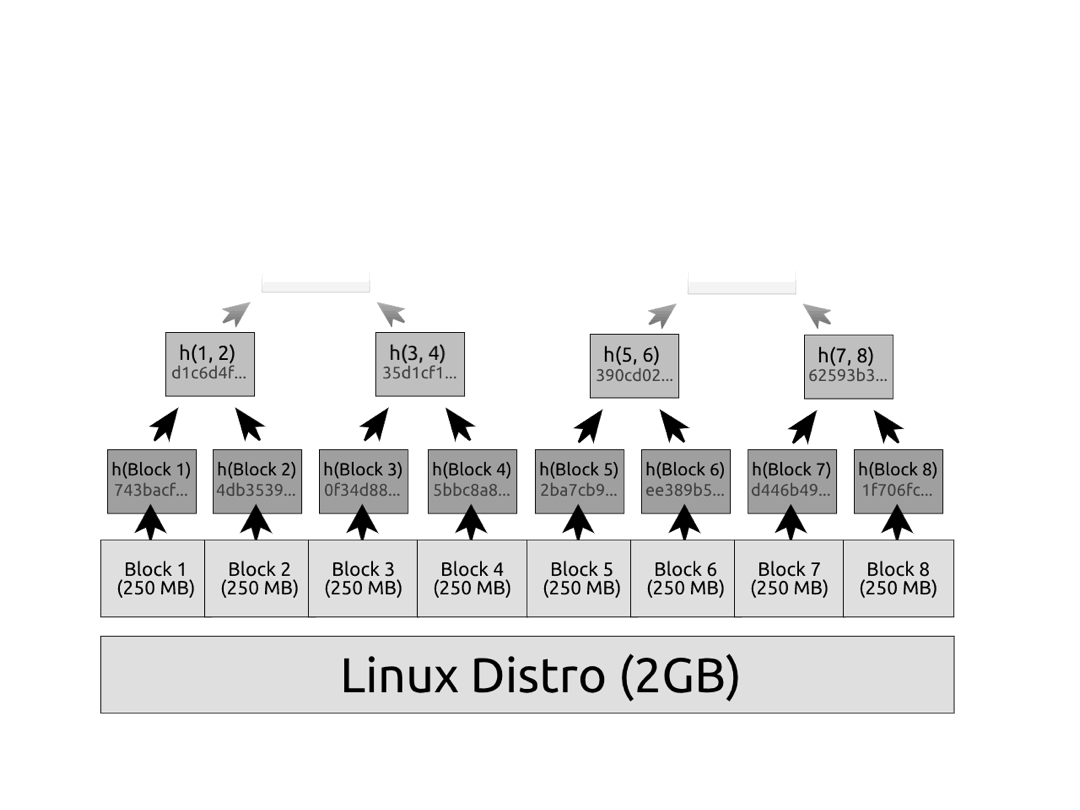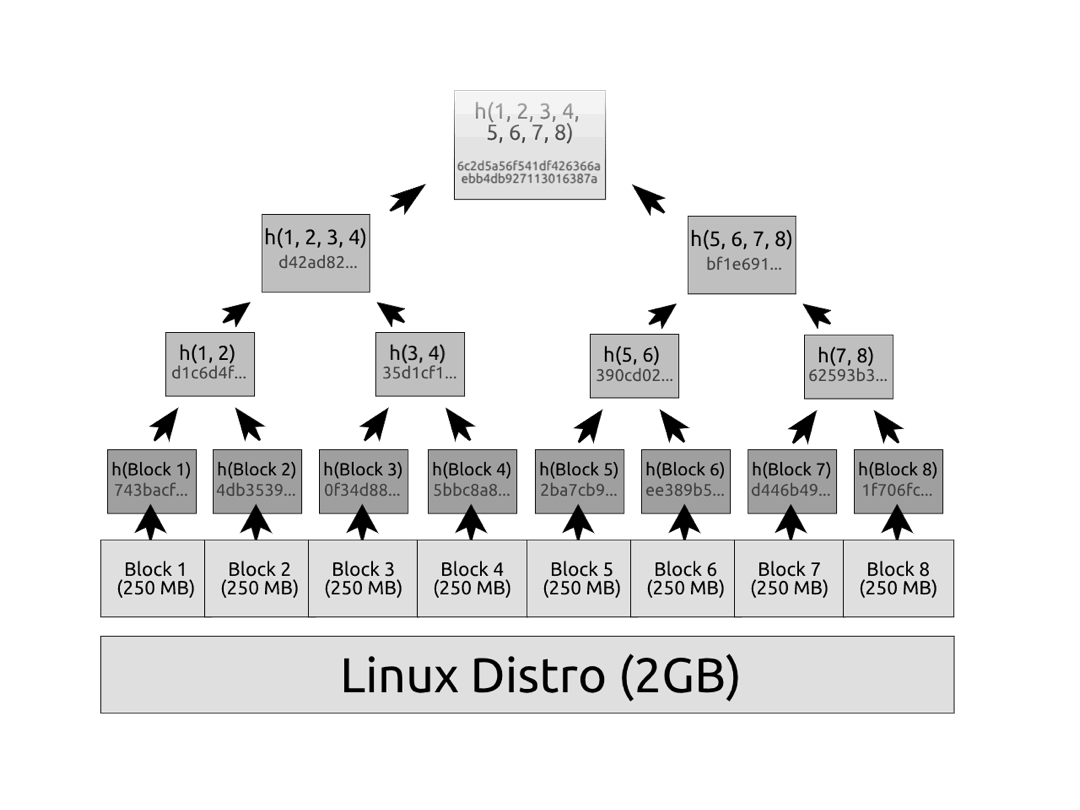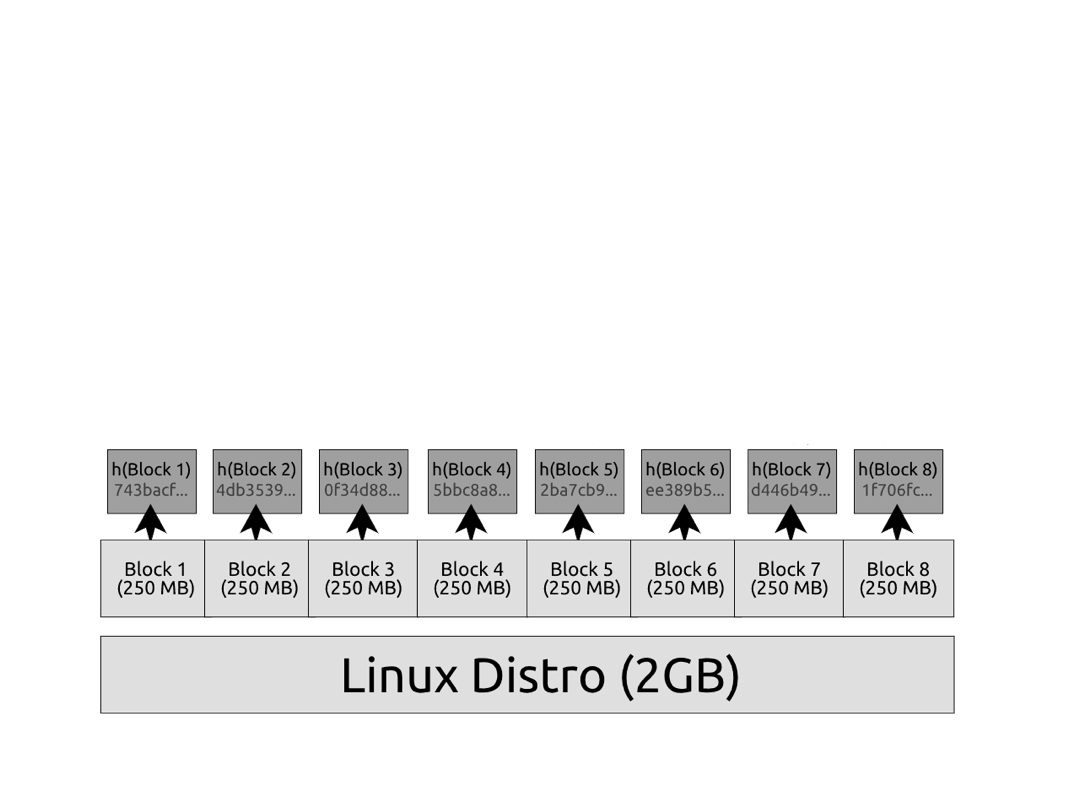
所以这棵树的根是 6c2d5a56f541df426366aebb4db927113016387a。注意，如果你修改了树中的任何元素，即使只是一位，哈希的雪崩效应会导致上游的每个哈希都发生变化，一直到根。

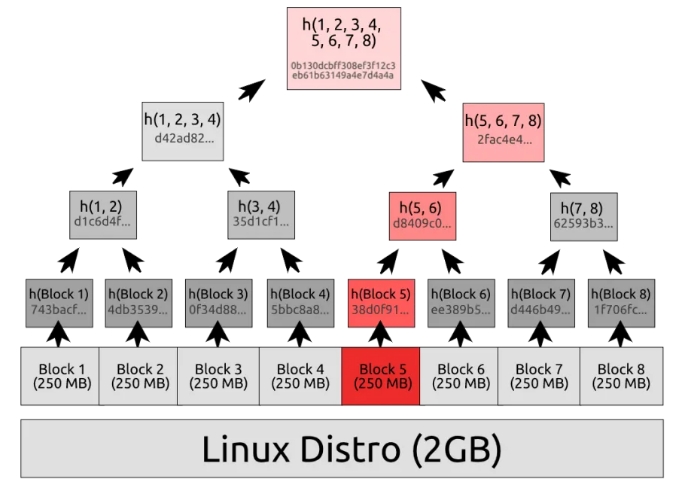
现在，假设我们下载了 Linux 发行版及其默克尔根（一个单一哈希）。我们在自己这边重新计算 Linux 发行版的默克尔树，发现我们的根与提供给我们的根不匹配。这意味着我们的文件已损坏。

我们如何快速诊断我们下载的哪个块是错误的？看看你能否自己找出答案。

答案是：我们必须请求规范默克尔树中根下的两个哈希，并找出哪个哈希与我们客户端的树不匹配。一旦我们找出哪个子树有问题，我们可以对该子树的两个子节点重复此操作，直到到达基底。假设只有一个错误块，这将使你只需进行   次比较（其中  是底层数据块的数量）即可定位该块。

包含证明

我们已经看到默克尔树在验证文件完整性方面的强大功能。但密码学累加器的真正力量不仅在于累加数据，还在于能够有效地证明关于数据的声明。

想象一个累加器是一个装满物品的不透明盒子。你不能直接查看这个盒子，但通过密码学的魔力，你可以以特定的方式查询它。

你可以用密码学累加器执行的操作之一是包含证明。这是一个小证明，明确证明某个项目存在于累加器中。

如果你知道一本电子书的默克尔根，我如何有效地向你证明某个引文来自那本电子书？我可以在不提供整本电子书甚至整个默克尔树的情况下做到这一点。

花点时间，看看你能否在不继续阅读的情况下勾画出如何做到这一点。有想法吗？下面的动画演示了一个简单的 4 字电子书的答案。

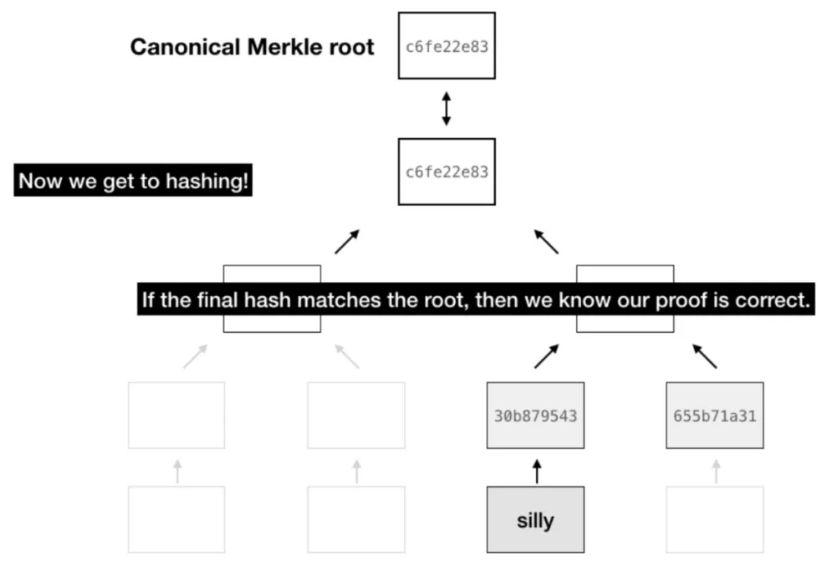
(原图太大)查看原gif图请移步https://learnblockchain.cn/article/9047

我们只需要提供我们要证明存在的数据、默克尔树根和从叶子到根路径上的兄弟哈希。这只需要  个哈希来传输。如果你重新进行所有哈希计算并且根匹配，你就可以确定该引用确实是电子书的一部分。这种证明被称为 默克尔证明。

你应该问：为什么这对于包含证明来说是足够的？如果有人只是编造兄弟哈希使根匹配怎么办？我们怎么知道它们来自真正的默克尔树？

我会留给你自己去思考。

比特币中的默克尔树

包含证明是由默克尔树启用的强大原语。它们在比特币轻客户端（也称为 SPV（简单支付验证）节点）中被广泛使用。我们将快速预览一下它是如何工作的。

在比特币中，过去约 10 分钟内发生的所有交易被捆绑在一起形成一个 区块 并传输给网络中的每个人。这些区块可能非常大，因为它们可能包含数千笔交易。

为了节省带宽，比特币采用了一个巧妙的技巧：传输的区块只包括该区块交易的默克尔树根。（实际上，这些传输的数据被称为 区块头，而交易本身则在请求时单独传输。我们稍后会详细了解这一点。）

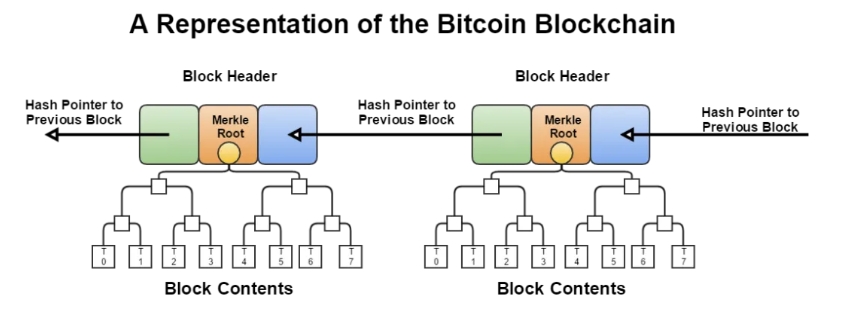
来源: LetsTalkBitcoin.com

由于默克尔树根是所有底层有序数据的加密累加器，每个区块头都包含对该区块中所有交易的承诺。由于这种优化，轻量级客户端只需要跟踪区块头，并且可以选择性地验证某笔交易是否包含在给定区块中的默克尔证明。这种优化对于移动电话或网页钱包能够使用比特币网络而无需下载所有内容至关重要。

如果这让你感到困惑，不要担心；比特币有很多结构，我们将在后续课程中解释。但到目前为止，你已经初步了解了默克尔树的用处。

关于默克尔树还有许多值得探索的创新，包括非包含证明、在线更新和 n 元默克尔树。如果你想了解最新技术的发展，我们将在附加阅读中提供资源。我们还将提供关于对默克尔树的一个天真实现进行的微妙的第二原像攻击的阅读材料（尽管在区块链环境中没有实际用途）。

作业

在我们的 **下一个作业**[5] 中，你将编写自己的默克尔树实现。然后你将编写代码来验证默克尔证明。

保存你的代码，因为如果你选择实现默克尔树，它可能对你的加密货币项目有用。

完成编码作业后，你就可以继续下一步了。

附加阅读

对默克尔树的第二原像攻击[6] by Dean Jerkovich (2018)

稀疏默克尔树[7]，允许高效的非包含证明 by Faraz Haider (2018)

Merkle. Mountain Ranges[8] by Ignotus Peverell (2018)

理解Merkle pollards[9]，使重复证明更高效 by Jim McDonald (2019)

以太坊中的默克尔[10] by Vitalik Buterin (2015)

声明：本网站所有相关资料如有侵权请联系站长删除，资料仅供用户学习及研究之用，不构成任何投资建议！