什么是MPT树
MPT 全称是 Merkle Patricia Trie 或者 Merkle Patricia Tree, 是Merkle Tree 和 Patricia Tree 的混合物,它在以太坊中常常被用作状态树 和 区块树,存储树。
以下是三种树的介绍
状态树 State Trie
每个以太坊账户都有一个与之对应的状态条目,包含账户地址,余额,代码和存储数据。
区块树 Block Trie
存储所有区块的哈希值。每个叶子结点代表一个区块的哈希值,每个父结点代表它下面的两个子节点的哈希值。
存储树 Storage Trie
用于存储以太坊合约中的数据,包括变量,映射和数组等,每个节点代表一个键值对。
在了解MPT树之前,我们先简单了解一下Merkle Tree 和 Patricia Tree 的各自的特点
Merkle Tree
其主要特点为:
● 最下面的叶节点包含存储数据或其哈希值;
● 非叶子节点(包括中间节点和根节点)都是它的两个孩子节点内容的哈希值。
默克尔树逐层记录哈希值的特点,让它具有了一些独特的性质。例如,底层数据的任何变动,都会传递到其父节点,一层层沿着路径一直到树根。
这些特性我们一般都能如何应用
证明某个集合中存在或不存在某个元素
通过提供该元素各级兄弟节点中的Hash值,可以不暴露集合完整内容而证明某元素存在
快速比较大量数据
因为每组数据排序后构建默克尔树结构。当两个默克尔树根相同时,则意味着所代表的两组数据必然相同
快速定位修改
一棵默克尔树,任何节点被修改,最终都会导致root节点的结果被修改。只要找到被修改的路径就可以知道哪条路径出了问题
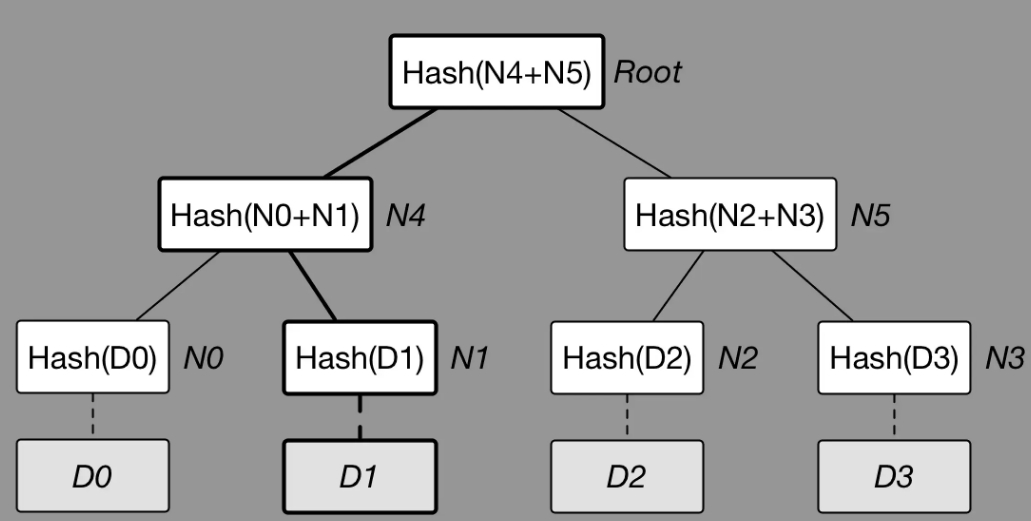
如图所示,D2 被修改了,受到影响的是 N2,D5,Root。因此可以快速定位问题路径。
通过Merkle Tree 树的这个特性,被用来作为交易树的存储结构,通过这个交易数,可以进行Merkle Proof进行数据的校验
Patricia Tree
到Patricia Tree ,就不得不提一下Radix Tree,两者都属于前缀树的变种。但两者还是有一些差异点
Patricia Tree 是一种压缩的二进制前缀树。它减少了每个节点的分支数,通常用于存储和查找二进制串,特别适合用于IP路由表或者其他长位串的匹配操作
Radix Tree 是通过压缩标准Trie来形成的,即合并只有一个子节点的节点。这样可以减少树的高度,优化查找操作的效率。
Patricia Tree的结构示意
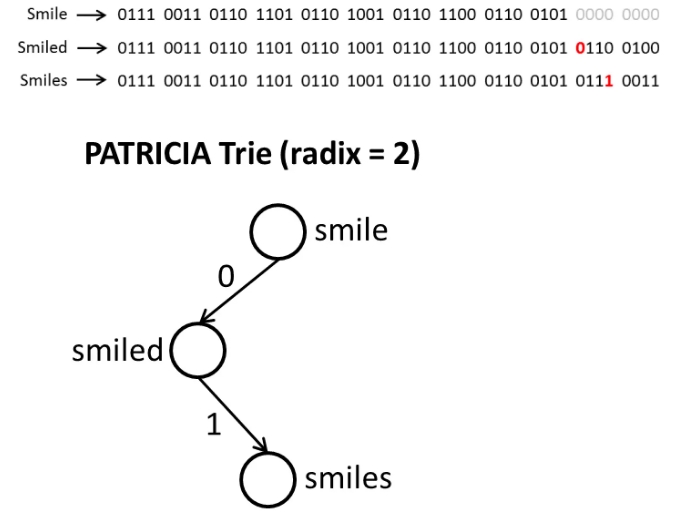
Radix Tree 的结构示意
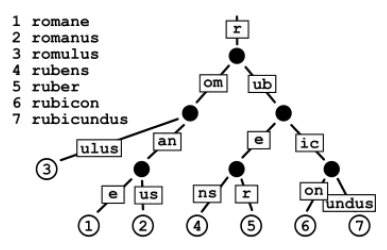
MPT 树
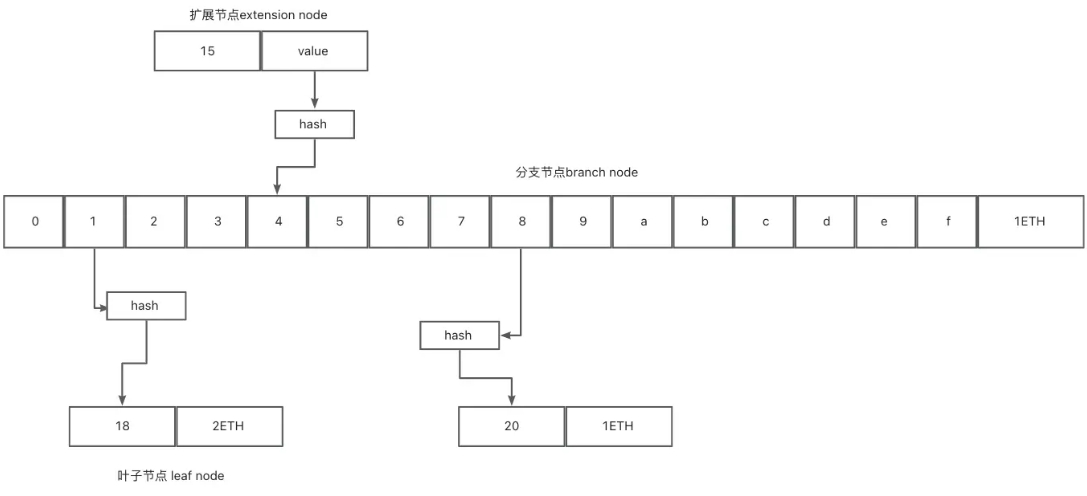
MPT 树的结构示意
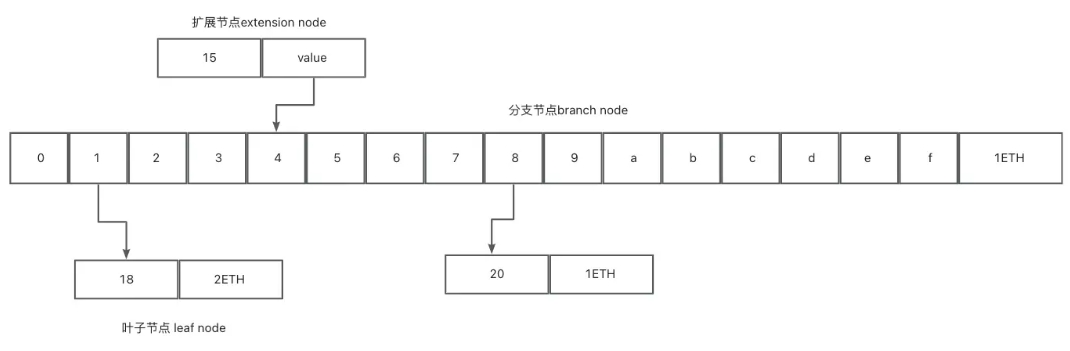
分支节点(branch node/full node):包含16个分支,以及1个value,它是一个长度为17的list,如果有一个[key,value]对在这个分支节点终止,最后一个元素代表一个值。否则也可以代表搜索路径的中间节点
扩展节点(extension node/short node):只有1个子节点,但是它的value是其他节点的hash值,主要是用来链接其他节点
叶子节点(leaf node):没有子节点,包含一个value, 其中key是一种特殊十六进制编码
MPT中的Merkle
指向下一级节点的指针是使用 节点的确定性加密hash,而不是下一级节点地址的指针,
这么做是用来防止攻击者的篡改,因为根哈希是公开的,任何人都可以 通过给定path上的所有节点,来证明在给定path上存在的定值,攻击者无法提供一个(key-value)对的证明,因为最终会影响到roothash
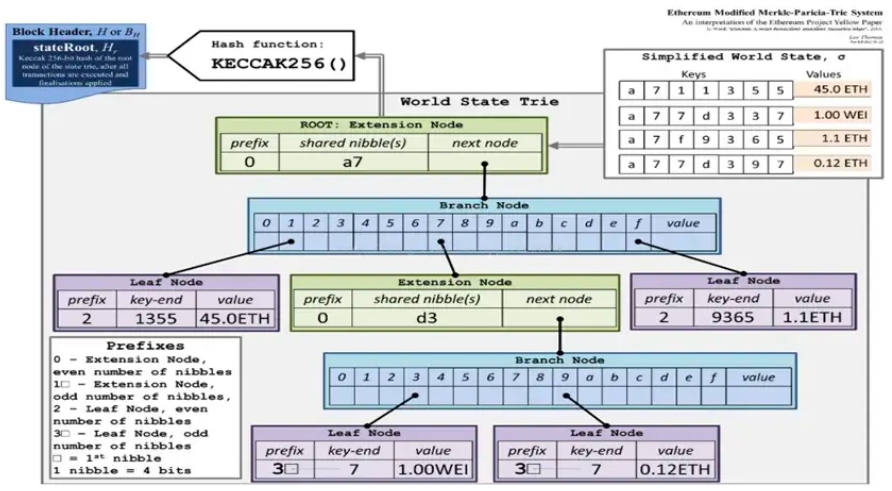
官方的表现形式
MPT 的增删改逻辑
新增
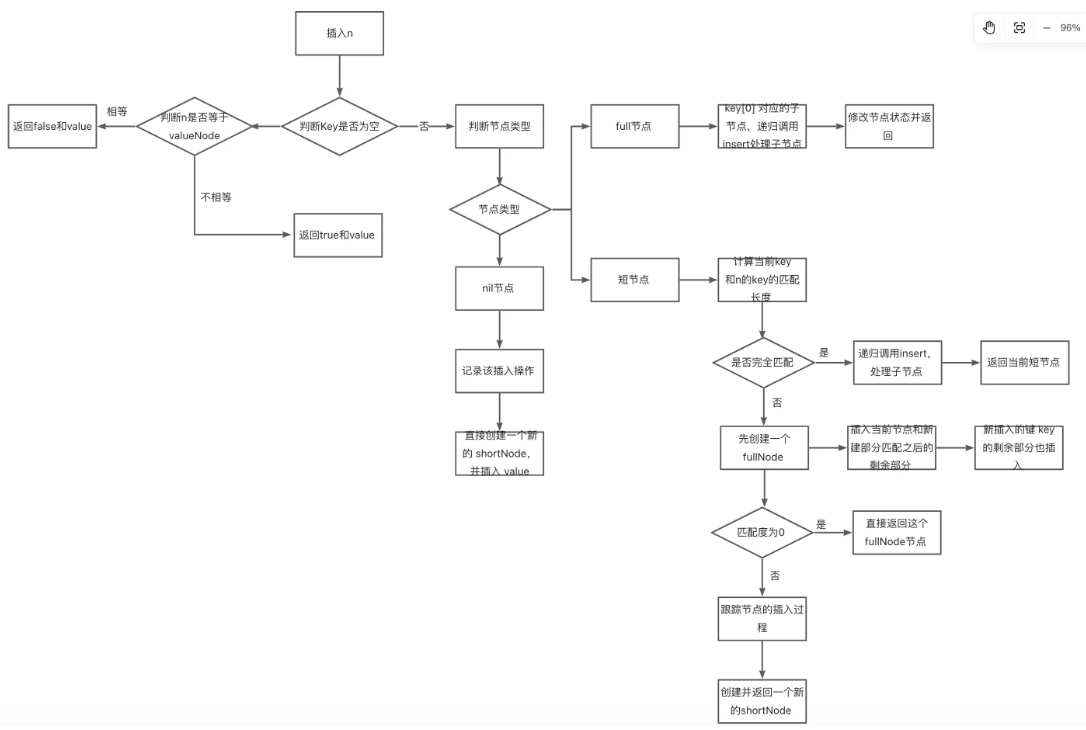
我们结合着代码一起来看
func (t *Trie) insert(n node, prefix, key []byte, value node) (bool, node, error) {
if len(key) == 0 { //意味着我们已经到达插入的最终位置
if v, ok := n.(valueNode); ok { // 需要先比较一下n是否与valueNode相等,只有不相等,才会更新
return !bytes.Equal(v, value.(valueNode)), value, nil
}
// 直接返回true 和vaule
return true, value, nil
}
switch n := n.(type) {
case *shortNode: 处理短节点
//计算当前键 key 与 shortNode 的键 n.Key 的前缀匹配长度
matchlen := prefixLen(key, n.Key)
// 如果整个key都匹配,则只更新对应的value
// and only update the value.
if matchlen == len(n.Key) {
// 递归调用 insert,继续处理子节点。
dirty, nn, err := t.insert(n.Val, append(prefix, key[:matchlen]...), key[matchlen:], value)
if !dirty || err != nil {
return false, n, err
}
return true, &shortNode{n.Key, nn, t.newFlag()}, nil
}
// key不匹配的情况下要创建一个fullNode.
branch := &fullNode{flags: t.newFlag()}
var err error
// 首先将当前短节点(shortNode)中和新建部分匹配之后的剩余部分,插入到新的分支节点的合适位置中。
_, branch.Children[n.Key[matchlen]], err = t.insert(nil, append(prefix, n.Key[:matchlen+1]...), n.Key[matchlen+1:], n.Val)
if err != nil {
return false, nil, err
}
// 然后,将新插入的键 key 的剩余部分 (key[matchlen+1:]) 插入到新创建的分支节点中。
_, branch.Children[key[matchlen]], err = t.insert(nil, append(prefix, key[:matchlen+1]...), key[matchlen+1:], value)
if err != nil {
return false, nil, err
}
// 直接返回创建好的分支节点 branch
if matchlen == 0 {
return true, branch, nil
}
// 用于跟踪节点的插入过程。传递的路径是从根节点到当前插入节点的路径,以便调试和日志记录
t.tracer.onInsert(append(prefix, key[:matchlen]...))
// 如果匹配的前缀不为 0,即 matchlen > 0,需要创建一个新的短节点 shortNode,它的键是当前键和新键的公共前缀部分 key[:matchlen],并且指向新创建的分支节点 branch
return true, &shortNode{key[:matchlen], branch, t.newFlag()}, nil
case *fullNode: // 处理full节点
// key[0] 对应的子节点,递归调用 insert,继续处理剩余的键 key[1:]
dirty, nn, err := t.insert(n.Children[key[0]], append(prefix, key[0]), key[1:], value)
if !dirty || err != nil {
return false, n, err
}
// 修改节点的状态
n = n.copy()
n.flags = t.newFlag()
// 将递归插入过程中返回的新的子节点 nn 更新到当前节点的相应子节点位置,即 Children[key[0]]
n.Children[key[0]] = nn
return true, n, nil
case nil:
// 记录该插入操作。
t.tracer.onInsert(prefix)
// 直接创建一个新的 shortNode,并插入 value
return true, &shortNode{key, value, t.newFlag()}, nil
case hashNode:
// We've hit a part of the trie that isn't loaded yet. Load
// the node and insert into it. This leaves all child nodes on
// the path to the value in the trie.
// 先加载节点资源
rn, err := t.resolveAndTrack(n, prefix)
if err != nil {
return false, nil, err
}
// 插入节点
dirty, nn, err := t.insert(rn, prefix, key, value)
if !dirty || err != nil {
return false, rn, err
}
// 返回新的节点信息
return true, nn, nil
default:
panic(fmt.Sprintf("%T: invalid node: %v", n, n))
}修改
更新逻辑相对比较简单,就不写流程图了
核心逻辑是value不为空,直接执行插入操作,更新root。value为空,执行删除操作,更新root
func (t *Trie) update(key, value []byte) error {
t.unhashed++ //增加未hash计数,这个计数器可能是用来追踪修改操作的次数或未计算哈希的节点数量
k := keybytesToHex(key) // key 转换为16进制
if len(value) != 0 { //如果 value 不为空,执行插入操作
_, n, err := t.insert(t.root, nil, k, valueNode(value))
if err != nil {
return err
}
t.root = n
} else { // 如果 value 为空,执行删除操作
_, n, err := t.delete(t.root, nil, k)
if err != nil {
return err
}
t.root = n // 更新root
}
return nil
}删除
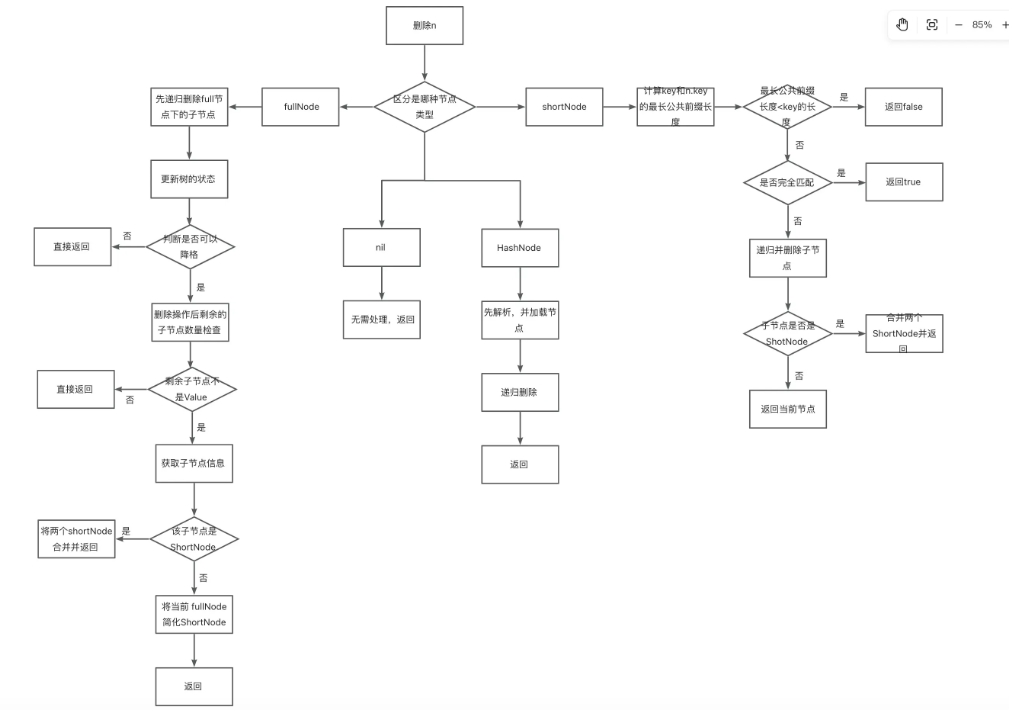
func (t *Trie) delete(n node, prefix, key []byte) (bool, node, error) {
// 区分是哪种节点
switch n := n.(type) {
case *shortNode:
// 计算当前key和n.key的最长公共前缀长度
matchlen := prefixLen(key, n.Key)
if matchlen < len(n.Key) { //如果最长公共前缀长度<key的长度,表示不匹配,直接返回false
return false, n, nil // don't replace n on mismatch
}
if matchlen == len(key) { // 如果完全匹配
// 将其标记为删除
t.tracer.onDelete(prefix)
// 返回true
return true, nil, nil // remove n entirely for whole matches
}
// 部分匹配,需要递归删除子节点
dirty, child, err := t.delete(n.Val, append(prefix, key[:len(n.Key)]...), key[len(n.Key):])
if !dirty || err != nil {
return false, n, err
}
switch child := child.(type) {
// 合并两个shortNode
case *shortNode:
t.tracer.onDelete(append(prefix, n.Key...))
return true, &shortNode{concat(n.Key, child.Key...), child.Val, t.newFlag()}, nil
default:
return true, &shortNode{n.Key, child, t.newFlag()}, nil
}
case *fullNode:
// 先递归删除full节点下的子节点
dirty, nn, err := t.delete(n.Children[key[0]], append(prefix, key[0]), key[1:])
if !dirty || err != nil {
return false, n, err
}
// 更新树的状态
n = n.copy()
n.flags = t.newFlag()
n.Children[key[0]] = nn
//如果 nn != nil,说明删除操作后,n 这个 fullNode 仍然有至少两个非空子节点(因为删除之前至少有两个子节点,现在还剩下一个非空的 nn,所以它仍然是 fullNode)
// 这一步,意味着不能将其降格为shortNode,直接返回即可
if nn != nil {
return true, n, nil
}
// 删除操作后剩余的子节点数量检查:
pos := -1
// 遍历 n.Children,查看还剩下多少个非空子节点
for i, cld := range &n.Children {
if cld != nil {
if pos == -1 {
pos = i
} else {
pos = -2
break
}
}
}
if pos >= 0 {
// 如果剩下的子节点不是存储值(即不是第 17 个子节点),那么可以尝试将 fullNode 简化为 shortNode
if pos != 16 {
// 来获取子节点的信息
cnode, err := t.resolve(n.Children[pos], append(prefix, byte(pos)))
if err != nil {
// 如果报错则直接返回
return false, nil, err
}
// 如果该子节点是 shortNode,则将该 shortNode 与当前节点合并
if cnode, ok := cnode.(*shortNode); ok {
t.tracer.onDelete(append(prefix, byte(pos)))
k := append([]byte{byte(pos)}, cnode.Key...)
return true, &shortNode{k, cnode.Val, t.newFlag()}, nil
}
}
// 否则,将当前 fullNode 简化为一个 shortNode
return true, &shortNode{[]byte{byte(pos)}, n.Children[pos], t.newFlag()}, nil
}
// n still contains at least two values and cannot be reduced.
return true, n, nil
// 直接返回 true 和 nil,表示删除成功
case valueNode:
return true, nil, nil
//空节点,无需处理
case nil:
return false, nil, nil
// 如果遇到的是一个尚未加载的哈希节点,则先解析并加载对应的节点,然后递归删除。
case hashNode:
rn, err := t.resolveAndTrack(n, prefix)
if err != nil {
return false, nil, err
}
dirty, nn, err := t.delete(rn, prefix, key)
if !dirty || err != nil {
return false, rn, err
}
return true, nn, nil
default:
panic(fmt.Sprintf("%T: invalid node: %v (%v)", n, n, key))
}
}声明:本网站所有相关资料如有侵权请联系站长删除,资料仅供用户学习及研究之用,不构成任何投资建议!